Расчёт общего резервирования с постоянно включенным резервом и с целой кратностью m при отсутствии последействия

Схема расчёта общего постоянного резервирования с целой кратностью m при отсутствии последействия при заданных вероятностях безотказной работы основного (Р ₀) и резервного (Р_N) элементов надёжности приведена на рисунке 5.5, а.

Система с общим резервированием будет нормально функциониро­вать при сохранении работоспособности хотя бы одной из цепей. На основании теоремы умножения вероятностей вероятность отказа такой системы

(5.4)

где Q_J - вероятность отказа J -ой цепи, состоящей из N элементов, а m - количество резервных цепей. Рисунок 5.5, а соответствует значению N = 1. Схема расчёта общего постоянного резервирования с целой кратностью m при отсутствии последействия при заданных вероятностях безотказной работы i -ых элементов надёжности основной (Р _{0 i}) и резервной (Р_Ji) цепей приведена на рисунке 5.5, б (1 ≤ i ≤ N).

Вероятность безотказной работы системы с общим резервированием рассчитывают по формуле

(5.5)

где Р_J - вероятность безотказной работы J -ой цепи.

Видно, что параллельное включение элементов является эффектив­ным средством повышения надёжности объекта. Значения вероятности безотказной работы Р_J одного элемента и вероятности безотказной работы системы Р_c для элементов с различной надёжностью приведены в таблице 5.1.

Таблица 5.1- Значения вероятности безотказной работы Р_J одного элемента и вероятности безотказной работы системы Р_c для элементов с различной кратностью резервирования [4]

РJ	Рc при
m = 1	m = 2	m = 3
0,50 0,70 0,90 0,95 0,99	0,75 0,91 0,99 0,9975 0,9999	0,875 0,973 0,999 0,999 0,999999	0,9375 0,9919 0,9999 0,99999 0,99999999

При экспоненциальном законе надёжности

(5.6)

где λ_J - интенсивность отказов J -ой цепи.

При равнонадёжных цепях и (λ_J = λ ₀) и экспоненциальном законе надёжности вероятность безотказной работы системы с общим резервированием рассчитывают по формуле

(5.7)

Средняя наработка до отказа одного элемента определяется через интенсивность отказов

Т ₀ = 1 / λ ₀. (5.8)

Средняя наработка до отказа системы с общим резервированием рассчитывают по формуле (3.17)

(3.17)

При преобразовании формулы (3.17) с учётом (5.7) и (5.8) получим [4, 19]:

(5.9)

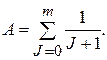(5.9 а)

Ниже приведены значения А для различных m:

m
А	1,5	1,83	2,08	2,28	2,45

Дисперсия средней наработки до отказа системы определяется по формуле [8, 19]:

(5.10)

Безотказная работа J -ой цепи будет иметь место при безотказной работе каждого из N последовательно соединенных элементов цепи. С учётом этого при экспоненциальном законе надёжности имеем

(5.11)

где Р_Ji - вероятность безотказной работы, а λ_Ji - интенсивность отказов i -ых элементов надёжности J -ой цепи.

Подставляя значения Р_J из выражения (5.11) в формулу (5.5), нахо­дим вероятность безотказной работы системы с общим резервированием

(5.12)

При равнонадёжных цепях вероятность безотказной работы системы с общим резервированием рассчитывают по формуле

(5.13)