Расчёт резервирования замещением для случаев облегченного резерва, ненагруженного резерва и общего нагруженного резервирования с последействием

Схемы резервирования замещением приведены на рисунке 5.7.

Рас­чётные соотношения для общего резервирования замещением с целой крат­ностью для устройств любой кратности ре­зервирования позволяет получить рекуррентная формула [8]

(5.21)

где Р_{m +1}(t), Р_m (t) - вероятности безотказной работы резервированной системы кратности m + 1 и m соответ­ственно; P (t - τ) - вероятность безотказной работы ос­новной системы в течение времени (t - τ); a_m (τ) - час­тота отказов резервированной системы кратности m в момент времени τ.

Для получения рабочих формул необходимо выполнить интегрирование в правой части, подставив вместо P (t - τ) и a_m (τ) их значения в соответствии с выбранным законом распределения и состоянием ре­зерва.

Для случая общего резервирования с замещением вероятность безотказной работы и средняя наработка до отказа при экспонен­циальном законе надёжности и нагруженном состоянии резерва опре­деляются формулами (5.7) и (5.9). Для облегченного резерва с замещением вероятность безотказной работы и средняя наработка до отказа при экспонен­циальном законе надёжности и при идеальных (безотказных) переключателях равны [4, 8]:

(5.21 а)

(5.22)

где λ_Н - интенсивность отказов резервного устройства до замещения.

При ненагруженном состоянии резерва с замещением вероятность безотказной работы и средняя наработка до отказа при экспонен­циальном законе надёжности равны [4, 8]:

(5.23)

(5.24)

 

где λ ₀ и Т _{1 0} - интенсивность отказов и средняя наработка до отказа основного (нерезервированного) устройства.

Для случая раздельного резервирования замещением при нагруженном состоянии резерва вероятность безотказной работы P _НЗ(t) и средняя наработка до отказа Т _НЗ при экспонен­циальном законе надёжности рассчитываются по формулам (5.15) - (5.17).

Принципиально возможно определить надёжность системы при резервировании замещением без использования рекуррентной формулы методами теории массового обслуживания (ТМО). Однако, в ряде случаев, полученные в результате этого расчётные формулы могут быть неточными и не пригодными для практических расчётов из-за принятых в этой теории допущений.

Покажем это для случая расчёта надёжности при резервировании замещением, когда интенсивности отказов основного и резервного элементов не равны по величине. Для этого случая мы решим лишь задачу резервирования замещением с кратностью резерви­рования резерва один к одному, то есть задачу с дублированием.

Пусть имеется система из одного рабочего и одного резервного невос­станавливаемых элементов. Резервирование ненагруженное замещением. Полагаем, что переключатели абсолютно надежны (Р п» 1). Требуется опре­делить надёжность системы методами теории массового обслуживания (ТМО). Интенсивность отказа основного элемента λ ₁, а резервного λ ₂.

Решение этой задачи будем проводить в следующем порядке:

а) изобразим граф всевозможных состояний системы (рисунок 5.8). На этом рисунке S ₀ – состояние, когда работает основной элемент, S ₁ - работает резервный элемент, так как основной отказал, S ₂ - система не работает, так как отказали оба элемента. Поскольку элементы не восстанавливаемые - стрелки на графе направлены только в одну сторону;

б) составим систему дифференциальных уравнений для состояний S ₀, S ₁, S ₂ по инженерному правилу А. Н. Колмогорова:

dP ₀(t) / dt = - λ ₁ · P ₀(t), (5.25)

dP ₁(t) / dt = λ ₁· P ₀(t) - λ ₂· P ₁(t), (5.26)

dP ₂(t) / dt = λ ₂· P ₁(t). (5.27)

Так как резерв ненагруженный, то можно считать, что резервный элемент свой резерв не расходует, пока работает основной элемент. В момент отказа нельзя считать dP_k / dt = 0 и переходить к системе алгебраических уравнений. Нужно решать дифференциальные уравнения известными в математике мето­дами. Подставив в первое и второе уравнения P ₀(t) = exp(- λ ₁· t), получим:

dP ₀(t) / dt = - λ₁ · exp(- λ ₁ · t); (5.28)

dP ₁(t) / dt = λ₁ · exp(- λ ₁· t) – λ ₂ · P ₁(t). (5.29)

Последнее дифференциальное уравнение для Р ₁(t) является линейным и методика решения его известна. Вначале запишем однородное уравнение

dP ₁(t) / dt + λ ₂ · P ₁(t) = 0. (5.30)

Разделяем в нём переменные

dP ₁(t) / P ₁(t) = – λ ₂ dt (5.31)

и при его интегрировании получаем

ln P ₁(t) = – λ ₂ × t +ln C, (5.32)

где ln C - постоянная интегрирования.

Учитывая свойства логарифма, получаем

P ₁(t) = С · exp(- λ ₂ · t). (5.33)

Ищем общее решение уравнения (5.29) в виде

P ₁(t) = С (t) · exp(- λ ₂ · t). (5.34)

Дифференцируя, имеем

dP ₁(t) / dt = (dС (t) / dt) · exp(- λ ₂ · t) - λ ₂· С (t) · exp(- λ ₂ · t). (5.35)

Подставив, выражения для P ₁(t) и dP ₁(t) / dt в уравнение (5.29), получим

(dС (t) / dt) · exp(- λ ₂ · t) - λ ₂· С (t) · exp(- λ ₂ · t) + λ ₂· С (t) · exp(- λ ₂ · t) =

= λ ₁· exp(- λ ₁ · t). (5.36)

(dС (t) / dt) = λ ₁· exp[(λ ₂ - λ ₁) · t ]. (5.37)

При интегрировании последнего выражения получаем

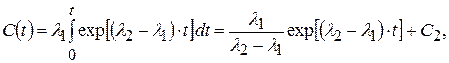(5.38)

где С ₂- постоянная интегрирования.

Подставив в общее решение уравнения (5.29) найденное значение С (t), получим

(5.39)

Для определения постоянной интегрирования учтём, что при t = 0 Р ₀(t) = Р ₀(0) = 1, а значит по условию нормировки вероятности других состояний при t = 0 равны нулю [ Р ₁(0) = Р ₂(0) = 0]. Тогда последнее выражение примет вид

P ₁(0) = 0 = [ λ ₁ / (λ ₂ - λ ₁)] + С ₂. (5.40)

Откуда

С ₂ = λ ₁ / (λ ₁ – λ ₂). (5.41)

И общее решение (5.39) уравнения (5.29) принимает вид

(5.42)

Следует отметить, что формулы (5.41) и (5.42) приближённые, так как при их выводе использовано инженерное правило А. Н. Колмогорова, установленное с использованием приближённого равенства

ехр(- λ · t) ≈ 1 – λ · t, (5.43)

справедливого лишь при значениях λ · t намного меньше единицы. С учётом приближённого равенства (5.43) формула (5.42) примет вид

(5.44)

в) найдя Р ₁(t), определим вероятность безотказной работы системы Р (t) с учётом приближённого равенства (5.43):

Р (t) = P ₀(t) + P ₁(t) = exp(- λ ₁· t) + λ ₁· t = 1- λ ₁· t + λ ₁· t = 1; (5.45)

г) находим из нормировочного условия вероятность отказа системы:

Р ₃(t) = 1 – Р (t) = 1 - 1 = 0. (5.46)

В результате видно, что для данной задачи расчёт с использованием системы дифференциальных уравнений для состояний S ₀, S ₁, S ₂, составленных по инженерному правилу А.Н. Колмогорова, даёт слишком грубый результат, не пригодный для использования на практике, так как при выводе правила А.Н. Колмогорова при разложении ехр(- λ · t) в ряд не учтены члены, содержащие (- λ · t)², (- λ · t)³, (- λ · t)⁴ и т. д.

Поэтому при решении сложных задач расчёта надёжности для случаев ненагруженного и облегчённого резервирования замещением, а также резервирования замещением с учётом последействия целесообразно использовать рекуррентную формулу (5.21), либо производить вычисления по схеме «гибели» с использованием преобразования Лапласа [8]. Если произвести расчёт не удаётся, то проводят испытания на надёжность на математических моделях, либо обычные испытания изделий на надёжность.

Рассмотрим пример расчёта надёжности для случая резервирования замещением с учётом последействия.

Пример 5.1 [8].

Две аккумуляторные батареи работают на одну нагрузку. Интенсивность отказов каждой из них λ = 0,1·10^-4 l/ час. При повреждении (отказе) одной из батарей интенсивность отказов исправной возрастает вследствие более тяжелых условий работы и равна λ ₁ = 0,8·10^-4 l/час. Необходимо найти вероятность без­отказной работы системы в течение времени t = 1000 час, а также среднее время безотказной работы.

Решение.

В нашем случае имеет место общее резер­вирование с постоянно включенным резервом. Так как при отказе одной батареи интенсивность отказов другой, исправной, изменяется, то имеет место последействие отказов. Дублированная система исправна в течение времени t при следующих благоприятных ситуациях:

А - ни одна из батарей за время t не отказала;

Б - аккумуляторная батарея 1 отказала, проработав время τ < t, а батарея 2 оставалась исправной в течение времени t;

В - аккумуляторная батарея 2 отказала, проработав время τ < t, а батарея 1 оставалась исправной в течение времени t.

Можно найти вероятность безотказной работы системы Р _С(t) как сумму вероятностей благоприятных гипотез, т.е.

Р _С(t) = Р _А(t) + Р _Б(t) + Р _В(t). (5.47)

Гипотезы Б и В одинаковы, поэтому Р _Б(t) = Р _В(t)и тогда

Р _С(t) = Р _А(t) + 2 Р _Б(t). (5.48)

Так как Р _А(t) есть вероятность того, что за время t ни одна из батарей не откажет, то

Р _А(t) = ехр(-2 λ · t). (5.49)

Вероятность гипотезы Б можно вычислить, восполь­зовавшись выражением

(5.50)

где a ₁(τ) · dτ - вероятность отказа первой батареи в мо­мент τ (вернее, в течение малого промежутка dτ); a ₁(τ) = λ · ехр(- λ ·t) - частота отказов первой батареи в момент τ; P ₂(τ) = ехр(- λ ·t) - вероятность безотказной работы аккумулятор­ной батареи 2 в течение времени τ, т.е. до отказа первой батареи; P ₂(t - τ) - вероят­ность безотказной работы батареи 2 за промежуток вре­мени от τ до t. Так как в этом промежутке интенсив­ность отказов батареи равна λ ₁, то

P ₂(t - τ) = ехр[- λ ₁×(t - τ)]. (5.51)

Подставляя все значения вероятностей в выражение (5.50) для Р _Б(t) и интегрируя, получаем

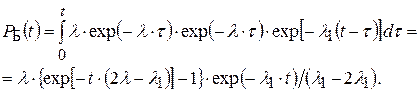(5.52)

Тогда вероятность безотказной работы резервирован­ной системы будет

Р _С(t) = Р _А(t) + 2 Р _Б(t) =

= ехр(- 2 λ · t) + 2 · λ ·{ехр[- t ×(2 λ - λ ₁)] -1}· [ехр(- λ ₁× t)] / (λ ₁ - 2 λ) =

= λ ₁· ехр(-2 λ · t) / (λ ₁ - 2 λ) - 2 λ · [ехр(- λ ₁ × t)] / (λ ₁ - 2 λ). (5.53)

Подставляя в эту формулу значения времени t = 1000 час, а также зна­чения интенсивностей отказов λ = 0,1·10^-4 l/час и λ ₁ = 0,8·10^-4 l/час, полу­чаем Р _С(t) ≈ 0,999.

Средняя наработка до отказа Т _1С определяется из соотношения (3.17)

(5.54)

Подставляя значения λ ₁ и λ, в эту формулу, имеем Т _1С = 62500 час.

Расчет надёжности резервированных систем иногда полезно выполнять, используя схему «гибели» («чистого размножения») [8]. В соответствии с этой схемой преобра­зование Лапласа вероятности возникновения n отказов вычисляется по формуле

(5.55)

При неравных корнях знаменателя обратное преоб­разование Лапласа Р _n(s) будет

(5.56)

В формулах (5.55) и (5.56) приняты обозначения: λ ₀ - интенсивность отказов системы до выхода из строя первого элемента; λ ₁ - интенсивность отказов системы в промежутке времени от момента отказа первого эле­мента до второго; λ ₂ - интенсивность отказов системы в промежутке времени от момента отказа второго эле­мента до третьего и т.д.; n - число отказавших элемен­тов; s_k = - λ_k - k -й корень знаменателя выражения (5.55); B '(s_k) - производная знаменателя в точке s_k.

При одинаковых опасностях отказов λ_ί, т.е. λ ₀ = λ ₁ = λ ₂ =…= λ_n, расчетные формулы имеют вид

(5.57)

При расчетах надёжности по формулам (5.55) - (5.57) следует помнить, что они не определяют вероят­ности безотказной работы (или вероятности отказа) резервированной системы, а определяют лишь вероят­ность n -го состояния системы, т.е. вероятность того, что в системе откажут n элементов. Для вычисления вероят­ности безотказной работы «необходимо находить вероят­ности 0, 1,..., n отказов, когда система еще находится в работоспособном состоянии (исправна), и суммиро­вать полученные вероятности.

Средняя наработка до отказа Т _1С системы при ис­пользовании схемы «гибели» вычисляется то

(5.58)

где λ_ί - интенсивность отказов системы до выхода из строя ί -го элемента.

Пример 5.2 [8].

Решить задачу, описанную в примере 5.1, используя для её решения схему «гибели».