Тема: изучениепоказателей надежности невосстанавливаемых и восстанавливаемых обьектов. Построение функций надежности, ненадежности, частоты и интенсивности отказов обьектов по теоретическому описанию случайной величины и статистической выборке наработок обьекта до отказа.
Схема выполнения задания:
· построить теоретическую и статистическую функции надежности;
· построить теоретическую и статистическую функции ненадежности;
· построить теоретическую и статистическую функции частоты отказов;
· построить теоретическую и статистическую функции интенсивности отказов.
Пример выполнения задания для распределения Релея в среде MathCAD11 приведен в прил. 4.
Приложение 1
Основные законы распределения НСВ
Экспоненциальное (показательное) распределение (область определения  )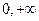
| ||
| Плотность распределения |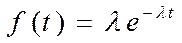 
| |
| Функция распределения |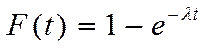 
| |
| Средняя наработка |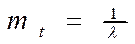  
| |
| Дисперсия наработки |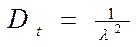 
| |
Нормальное распределение (распределение Гаусса) (область определения  )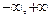
| ||
| Плотность распределения |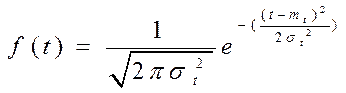 
| |
| Функция распределения |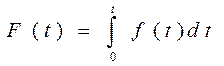 
| |
| Распределение Вейбулла (область определения )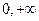
| ||
| Плотность распределения |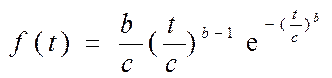 
| |
| Функция распределения |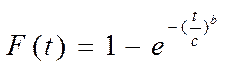 
| |
| Средняя наработка |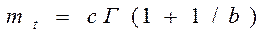 
| |
| Дисперсия наработки |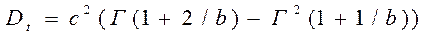 
| |
| Гамма-распределение (область определения )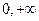
| ||
| Плотность распределения |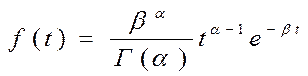 
| |
| Функция распределения |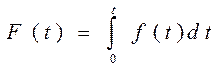 
| |
| Средняя наработка |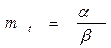 
| |
| Дисперсия наработки |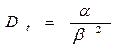 
| |
Окончание прил. 1
| Альфа-распределение (область определения )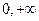
| ||
| Плотность распределения |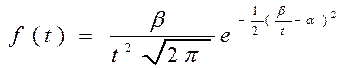 
| |
| Функция распределения |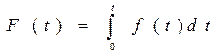 
| |
| Средняя наработка |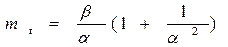 
| |
| Дисперсия наработки |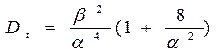 
| |
| Распределение Релея (область определения )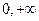
| ||
| Плотность распределения |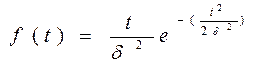 
| |
| Функция распределения |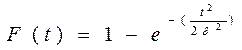 
| |
| Средняя наработка |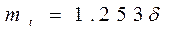 
| |
| Дисперсия наработки |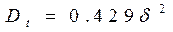 
| |
| Логарифмически-нормальное распределение (область определения )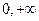
| ||
| Плотность распределения |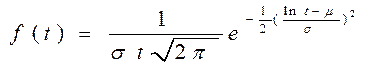 
| |
| Функция распределения |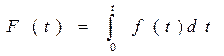 
| |
| Средняя наработка |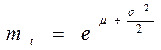 
| |
| Дисперсия наработки |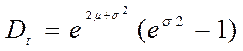 
| |
Бета-распределение (область определения  )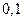
| ||
| Плотность распределения |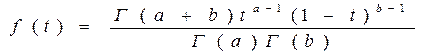 
| |
| Функция распределения |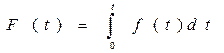 
| |
| Средняя наработка |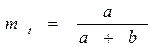 
| |
| Дисперсия наработки |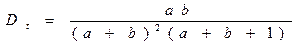 
| |
Приложение 2
Пример выполнения задания №1
1.Функция плотности распределения Релея.
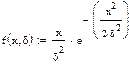
2. Функция распределения Релея.
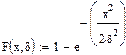
Продолжение прил. 2
3. Начальные моменты.
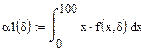
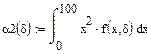
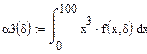
(1-ый начальный момент) (2-ой начальный момент) (3-ий начальный момент)
4. Математическое ожидание (1-ый начальный момент).
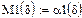
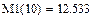
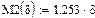
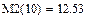
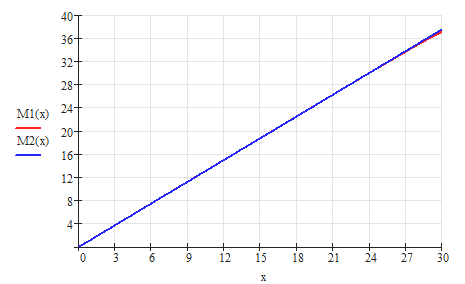
5. Мода (наиболее вероятное значение).
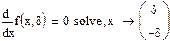
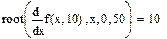
6. Медиана (50%-квантиль).
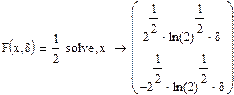
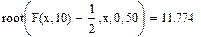
7. Дисперсия (второй центральный момент).
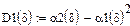
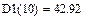
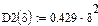
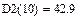
Окончание прил. 2
8. Среднеквадратическое отклонение.
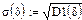
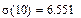
9. Коэффициент асимметрии.
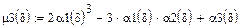(третий центральный момент)
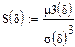
Приложение 3
Пример выполнения задания №2
1. Распределение Релея (функция плотности, функция распределения вероятностей).
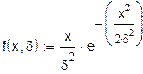
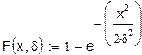
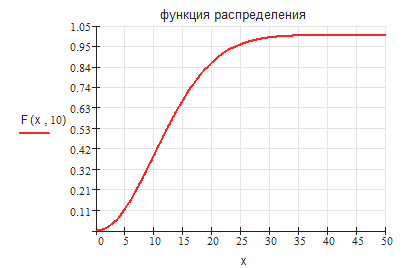
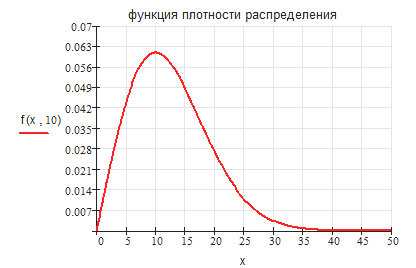
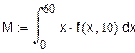
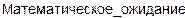
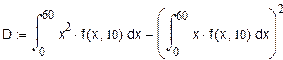
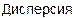
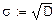
Продолжение прил. 3
2. Функциональные зависимости и параметры, полученные с помощью имитации распределения Релея методом обратных функций.
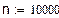
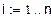
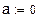
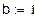
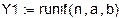
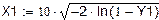
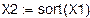
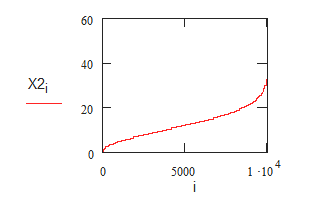
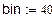
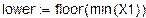
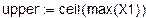
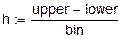
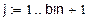
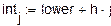
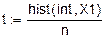
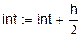
Окончание прил. 3
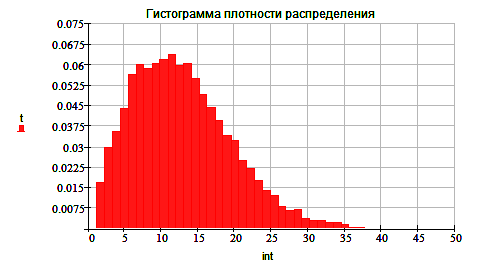
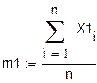
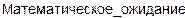
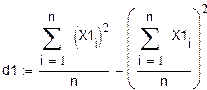
3. Сравнение результатов.
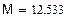
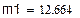
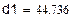
Приложение 4
Пример выполнения задания №3
1. Исходные данные для статистического анализа.
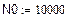(количество объектов, поставленных на испытание)
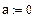
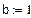
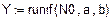
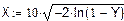
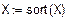
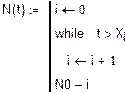
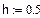
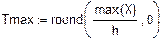
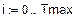
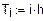
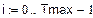
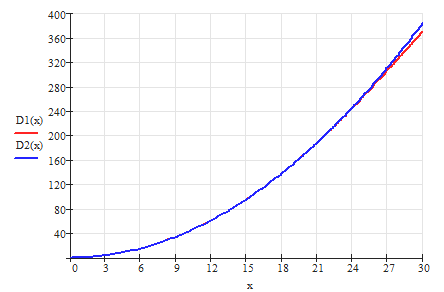
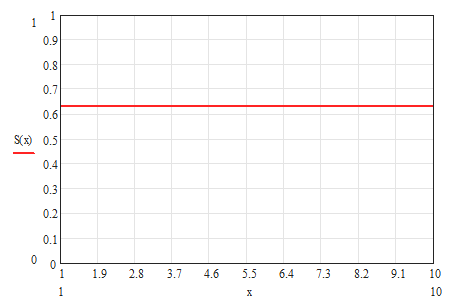
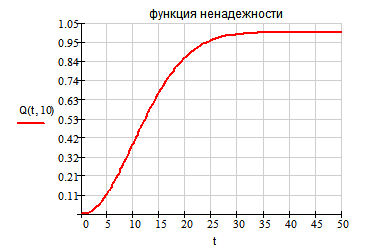
2. Функция надежности.
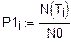
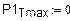
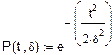
Теоретический вид
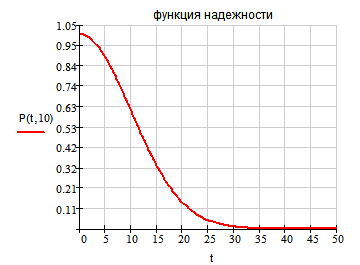
Продолжение прил. 4
Статистический вид
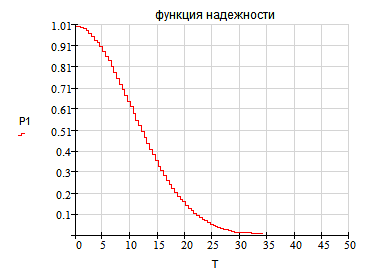
3. Функция ненадежности.
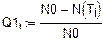
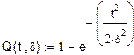
Теоретический вид
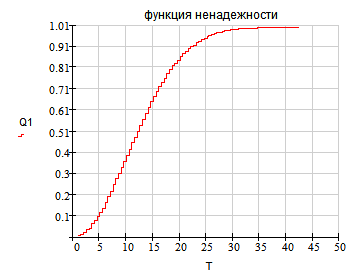
Продолжение прил. 4
Статистический вид
4. Функция частоты.
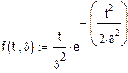
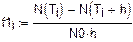
Теоретический вид
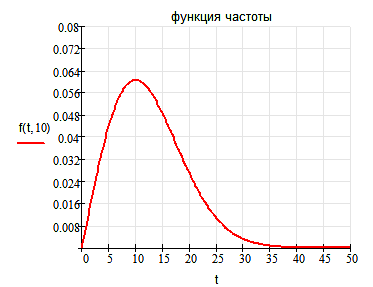
Продолжение прил. 4
Статистический вид
5. Функция интенсивности.
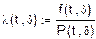
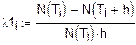
Теоретический вид
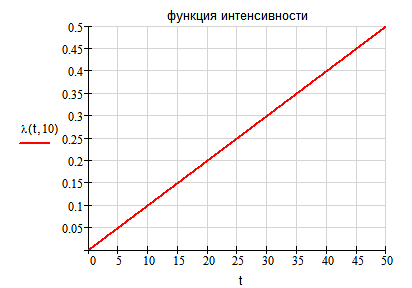
Окончание прил. 4
Статистический вид
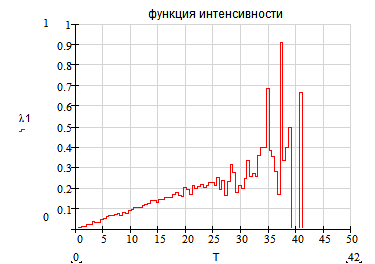
Приложение 5
Математические функции
| Наименование функции | Обозначение функции |
| Тригонометрические функции | |
| Синус | sin(x) |
| Косинус | cos(x) |
| Тангенс | tan(x) |
| Секанс | sec(x) |
| Косеканс | csc(x) |
| Котангенс | cot(x) |
| Показательные и логарифмические функции | |
| Экспоненциальная функция | eхр(x) |
| Натуральный логарифм (по основанию е) | 1n(x) |
| Десятичный логарифм (по основанию 10) | log(x) |
| Матричные функции | |
| Объединяет в одну матрицы Ml и М2, имеющие одинаковое число строк (объединение идет "бок о бок") | augment(Ml,M2) |
| Создает диагональную матрицу, элемент главной диагонали которой — вектор V | diag(V) |
| Возвращает число столбцов матрицы М | cols(M) |
| Возвращает число строк матрицы М | rows(M) |
| Возвращает среднее значение элементов массива М | mean(M) |
| Возвращает медиану элементов массива М | median(M) |
Приложение 6
Статистические функции
| Функция | Назначение |
| Функции вычисления плотности вероятности распределения | |
| dbeta(x, s1, s2) | Вета-распределение (s1, s2>0 — параметры формы, 0<x<1) |
| dchisq(x, d) | Хи-квадрат-распределение (х, d>0, причем d — число степеней свободы) |
| dexp(x, r) | Экспоненциальное распределение (r, х>0) |
| dgamma(x, s) | Гамма-распределение (s>0 — параметр формы, х³0) |
| dlnorm(x, m,s) | Логарифмически-нормальное распределение (m — натуральный логарифм среднего значения, s > 0 — натуральный логарифм среднеквадратичного отклонения, х>0) |
| dnorm(x,m,s) | Нормальное распределение (m — среднее значение, s > 0 — среднеквадратичное отклонение) |
| dunif(x, а, b) | Равномерное распределение (а и b — граничные точки интервала, причем а< b и а£ х£ b) |
| dweibull(x, s) | Распределение Вейбулла (s>0 — параметр формы) |
| Функции распределения | |
| pbeta(x, s1, s2) | Значение в точке х функции стандартного нормального распределения |
| pchisq(x, d) | Значение в точке х кумулятивного {Хи-квадрат-распределения, в котором d - степень свободы |
| рехр(х, r) | Значение в точке х функции экспоненциального распределения |
| pgamma(x,s) | Значение в точке х функции гамма-распределения |
| plnorm(x, m,s) | Значение в точке х функции логнормального распределения |
| plnonn(x, m,s) | Значение в точке х функции нормального распределения |
| punif(x, a, b) | Значение в точке х функции равномерного распределения |
| pweibull(x, s) | Значение в точке х функции распределения Вейбулла |
| Функции создания m - векторов различными законами распределения | |
| rbeta(m, s1, s2) | Вета-распределение |
| rchisq(m, d) | Хи-квадрат-распределение |
| rexp(m, r) | Экспоненциальное распределение |
| rgamma(m, s) | Гамма-распределение |
| rlnorm(m ,m,s) | Логарифмически-нормальное распределение |
| rnorm(m, m,s) | Нормальное распределение |
| runif(m, а, b) | Равномерное распределение |
| rweibull(m, s) | Распределение Вейбулла |
ЛИТЕРАТУРА
1. MathCad 6.0 Plus. Финансовые, инженерные и научные расчеты в среде Windows. Изд. 2. – М.: Информационно-издательский дом «Филинь», 1997.
2. Теория надежности радиоэлектронных систем в примерах и задачах / Под ред. Г.В. Дружинина. – М.: Энергия, 1976.
3. Вентцель Е.С. Теория вероятностей. – М.: Высш. шк., 1978.
4. Дружинин Г.В. Надежность автоматизированных систем. – М.: Энергия, 1977.
5. Козлов Б.А., Ушаков И.А. Справочник по расчету надежности. – М.: Сов. радио, 1966.
6. Барлоу Р., Прошин Ф. Математическая теория надежности. – М.: Сов. радио, 1969.
7. Гнеденко Б.В., Беляев Ю.К., Соловьев А.Д. Математические методы в теории надежности. – М.: Наука, 1965.
8. Голинкевич Т.А. Прикладная теория надежности: Учебник для вузов. – М.: Высш. шк., 1985.
9. Надежность технических систем: Справочник / Под ред. И.А. Ушакова. – М.: Радио и связь, 1985.
10. ГОСТ 17.002-89. Надежность в технике. Термины и определения.
11. ГОСТ 24.701.-86. ЕСС АСУ. Надежность автоматизированных систем управления. Основные положения.
12. ГОСТ 27310-95 (МЭК 812-85). Надежность в технике. Анализ видов, последствий и критичности отказов. Основные положения.
Св. план 2006, поз. 59
Учебное издание
Бахтизин Вячеслав Вениаминович,
Фадеева Елена Павловна
