Для решения системы уравнений необходимо выполнить следующее:
§ задать начальные приближения для всех неизвестных, входящих в систему уравнений;
§ напечатать ключевое слово Given. Оно указывает MathCAD11, что далее следует система уравнений. При печатании слова Given можно использовать любой шрифт, строчные и прописные буквы;
§ ввести уравнения и неравенства в любом порядке ниже ключевого слова Given. Удостовериться, что между левыми и правыми частями уравнений стоит символ “=” (“жирный” знак равенства; для его печати необходимо использовать [Ctrl] =). Между левыми и правыми частями неравенств может стоять любой из символов <, >, ≥, ≤;
§ ввести любое выражение, которое включает функцию Find. При печати слова Find можно использовать шрифт любого размера, произвольный стиль, прописные и строчные буквы. Find(z1, z2, z3, …) – возвращает решение системы уравнений. Число аргументов должно быть равно числу неизвестных (рис. 4.2).
Функция Find возвращает найденное решение следующим образом:
§ Если функция Find имеет только один аргумент, то она возвращает решение уравнения, расположенного между ключевыми словами Given и функцией Find;
§ Если функция Find имеет более одного аргумента, то она возвращает ответ в виде вектора. Например, Find(z1,z2) возвращает вектор, содержащий значения z1 и z2, являющиеся решением системы уравнений.
Что делать, когда MathCAD11 не может найти решения?
Если в результате решения уравнений на каком-либо шаге итераций не может быть найдено более приемлемое приближение к искомому решению по сравнению с предыдущим шагом, то поиск решения прекращается, а функция Find помечается сообщением об ошибке “ решение не найдено ”.
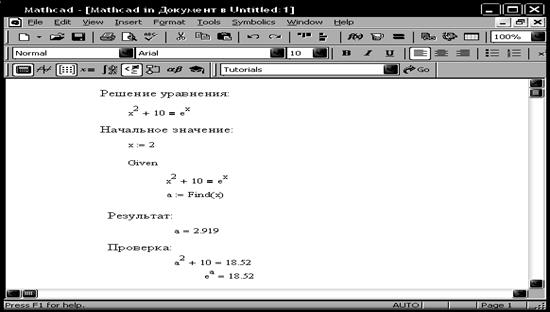
Рис. 4.2. Блок решения уравнений для одного уравнения с одним неизвестным
Причиной появления этого сообщения об ошибке может быть следующее:
§ поставленная задача не иметь решения;
§ для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число;
§ в процессе поиска решения последовательность приближений попала в точку локального минимума невязки;
§ в процессе поиска решения получена точка, которая не является точкой локального минимума, но из которой метод минимизации не может определить дальнейшее направление движения.






