Для решения уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение, переменная, входящая в выражение, и интервал, в котором ищется корень. Функция возвращает значение переменной, которое обращает выражение в нуль (рис. 4.1):
root (f(var1), x,[a, b]),
f(var1) – это либо функция, определенная в рабочем документе, или выражение, обращенное в нуль Выражение должно возвращать скалярное значение;
x – имя переменной, которое используется в выражении. Это та переменная, варьируя которую MathCAD11 будет пытаться обратить выражение в нуль;
[a, b] – интервал поиска корня; a и b должны быть действительными числами, a<b. Они являются необязательными параметрами.
Если интервал [a, b] не указан, то необходимо переменной x присвоить некоторое начальное значение до начала использования функции root.
MathCAD11 в функции root использует для поиска корня метод секущей. Значение a используется как начальное приближение при поиске корня (если иное не указано). Когда значение f(var1) приочередном приближении становится меньше значения встроенной переменной TOL (по умолчанию 0.001), корень считается найденным, и функция возвращает результат. Можно изменить точность, с которой функция root ищет корень, изменив значение встроенной переменной TOL. Например, присвоив TOL:=0.1.
Если функция root не сходится:
§ Уравнение не имеет корней;
§ Корни уравнения находятся вне интервала поиска, либо далеко от начального приближения;
§ Выражение имеет разрывы между начальным приближением и корнями;
§ Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.
Чтобы установить причину ошибки, следует исследовать график функции f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения.
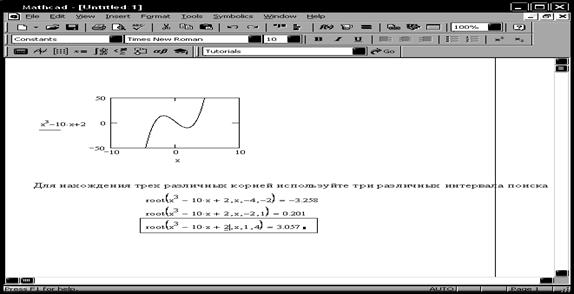
Рис. 4.1. Использование графика и функции root для поиска корней уравнения






