Рассмотрим в общих чертах некоторые из основных идей теории устойчивости.
Здесь масса 
удерживается упругой пружиной с жесткостью 
и амортизирующим демпфером, который создает вязкую силу 
, противоположную скорости 
.
Изображая график зависимости перемещения 
от времени 
, получаем картину затухающих колебаний, характерных для движения маятника в воздухе (см. рисунок).
Рисунок 1.61 - Поведение линейного осцилятора с затуханием
В фазовом пространстве переменных и 
имеется устойчивый фокус, переходящий в окружности или эллипсы для незатухающей системы.
Трехмерный график такого асимптотически устойчивого поведения показан на следующем рисунке в пространстве переменных , и .
Уравнение движения осциллятора имеет следующий вид:
.
Уравнение движения, отнесенное к массе и имеющее удобную стандартную форму 
. Экспоненциальное решение данного уравнения имеет вид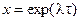 
, где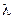 
– корни характеристического уравнения 
.
В рассматриваемом случае характеристическое уравнение квадратично по .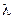
Решение зависит от корней характеристического уравнения, которые будут действительными или комплексными в зависимости от знака дискриминанта 
.
Если дискриминант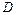 
положителен 
, имеются два действительных корня, и, как и предполагалось, решение ведет себя экспоненциально.
Если же дискриминант 
отрицателен 
, уравнение имеет два комплексно сопряженных корня и дает решение вида 
.
Таким образом, осциллятор с демпфером становится неустойчивым, если хотя бы один из корней имеет положительную действительную часть (рисунок 1.62).
Рисунок 1.62 - Траектории в случае устойчивого и неустойчивого фокуса: а – устойсивый фокус; б – неустойчивый фокус
При решении уравнения его наиболее часто представляют в следующем виде 
. Выражение для дискриминанта 
равно 
.
Если начальные условия заданы в виде: 
и 
при 
, то для случая, когда 
решение запишется:
,
а при 
– в виде
,
где 
.
Умножим каждый из членов уравнение на скорость (скорость) и после не сложных преобразований получим:
.
Величина, стоящая в скобках, – это с точностью до постоянного множителя полная энергия осциллятора.
При он равен начальной энергии осциллятора, которая зависит от его положения и начальной скорости. Член в правой части 
учитывает диссипацию энергии. Когда коэффициент 
положителен, то со временем полная энергия уменьшается до тех пор, пока не обратиться в нуль и линейный осциллятор при 
описывает затухающие колебания.
Однако коэффициент может быть и отрицательным в том случае если движение осциллятора порождает силы, увеличивающие это движение. Например, в клапанных механизмах подкачки энергии. При 
линейный осциллятор описывает нарастающие колебания или не колебательный уход от состояния равновесия.
Возможные типы поведения осциллятора изображены на рисунке. Если жесткость велика и затухание мало, то корни комплексные и имеется устойчивый фокус.
Если уменьшать жесткость в направлении горизонтальной стрелки, то, как только пересекается парабола критического затухания 
, корни становятся действительными и фазовый портрет превращается в устойчивый узел.
Нагрузка на упругую конструкцию может вызвать статическую потерю устойчивости, при которой эффективная жесткость системы меняется с положительной на отрицательную. Эта статическая неустойчивость, характеризуемая появлением смежного положения равновесия, изображается горизонтальной стрелкой.
Рисунок 1.63 - Фазовый портрет и структура корней для линейного осциллятора
Если же гибкая упругая конструкция подвергается силовому воздействию, скажем, ветра, то порыв ветра может вызвать галопирование конструкции, при котором эффективное затухание становится отрицательным, как показано вертикальной стрелкой.
При этой динамической неустойчивости устойчивый фокус переходит в неустойчивый, которому соответствует растущее колебательное движение. При движении вдоль каждой из стрелок перемещения линейной системы становятся бесконечными в точке перехода к неустойчивому режиму, однако на поведение реальной системы обычно оказывают влияние нелинейные эффекты. Этот вопрос мы будем обсуждать в следующем разделе.
Консервативная система без демпфирования с центром эллиптических траекторий в действительности представляет критический промежуточный случай между устойчивой и неустойчивой областями, и рассмотрение упругой устойчивости без демпфирования приводит к патологическим корням, изображенным на рис. а.
Любое положительное 
приводит к неустойчивости. Устойчивым системам соответствуют только точки положительного квадранта (рисунок 1.64 б).
Рисунок 1.64 - Механизмы неустойчивости ? – статическая неустойчивость; ™ – динамическая неустойчивость; ½ – упругая неустойчивость
Об этом часто забывают, и пренебрежение демпфированием, которое несущественно для некоторых консервативных систем, может привести к парадоксальным результатам для гироскопических и вращательных систем.
