Аттрактор. Множество точек или подпространство в фазовом пространстве, к которому приближается траектория после затухания переходных процессов. Классическими примерами аттракторов в динамике могут служить точки равновесия или неподвижные точки отображений, предельные циклы или поверхности торов для квазипериодических движений.
Бифуркация. Изменение характера движения динамической системы на большом временном интервале при изменении одного или нескольких параметров. Например, при сжатии стержня происходит выпучивание, и одно состояние равновесия, потеряв устойчивость, сменяется двумя новыми устойчивыми состояниями равновесия.
Возвращаясь к роли нелинейности, рассмотрим три статические бифуркации, показанные на рисунке. Они моделируют механическую систему типа шарика, катающегося по поверхности энергии, которая деформируется, если приложена нагрузка 
(рисунок 1.65).
Рисунок 1.65 - Три типа статических бифуркаций
В первой асимметричной точке бифуркации, наблюдаемой при потере устойчивости рам, минимум и максимум сливаются и затем снова расходятся.
Во второй устойчиво симметричной точке бифуркаций, известной конструкторам по поведению стержня Эйлера, исходный минимум переходит в широкую яму с маленьким пиком в центре.
Третья картина демонстрирует неустойчиво симметричную точку бифуркации, которая является обращением предыдущего случая и наблюдается при потере устойчивости арок и оболочек.
В каждой из этих бифуркаций, тривиальное равновесное состояние с нулевым перемещением 
становится неустойчивым при пересечении со вторичной равновесной траекторией. Это наблюдение находится в соответствии с недавно установленной теоремой, которая утверждает, что для консервативной системы нелинейная бифуркация, в которой нет предельной точки, всегда свидетельствует о неустойчивости.
Бифуркации в динамической системе. По мере изменения параметров динамической системы может меняться число точек равновесия и их устойчивость. Значения параметров, при которых изменяются качественные или топологические свойства движения, называются критическими или бифуркационными значениями.
Рассмотрим решение, описывающее идеальный осциллятор Дуффинга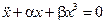 
. Для начала построим зависимость положения точек равновесия от 
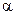. (рисунок 1.66)
С изменением 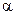от положительных до отрицательных значений единственная точка равновесия распадается на три. На языке динамики: единственный центр преобразуется в седловую точку в центре координат и два центра (рисунок 1.67). Бифуркация такого типа называется бифуркацией типа вил.
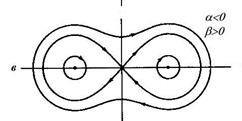
Рисунок 1.66 - Траектории осциллятора с нелинейной возвращающей силой (уравнение Дуффинга на фазовой плоскости: а – случай жесткой пружины; б – случай мягкой пружины; в – потенциал с двумя ямами)
Физический смысл этого явления понятен из того; что силу – 
можно описать с помощью потенциальной энергии. Когда 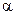становится отрицательным, потенциал с одной ямой заменяется потенциалом с двумя ямами. При этом происходит качественное изменение динамики системы, и поэтому 
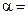0 является критическим бифуркационным значением.
Бифуркация Андронова – Хопфа (Бифуркация рождение цикла). Рождение предельного цикла из состояния равновесия при изменении некоторого названия. Свое название эта бифуркация получила в честь математика, сформулировавшего точные условия ее существования у динамической системы.
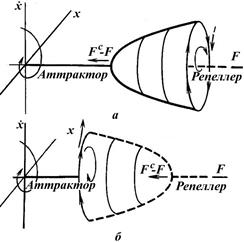
Рисунок 1.67 - Динамическая бифуркация нелинейного осциллятора: а – притягивающий предельный цикл D> 0; б –отталкивающий предельный цикл D< 0
Динамические точки бифуркации, вероятно, несколько менее известны; простой пример динамической бифуркации нелинейного осциллятора изображен на рисунке.
Здесь вместо симметричной за критической равновесной траектории имеется семейство растущих предельных циклов. Они рассматриваются в фазовом пространстве переменных 
и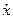 
при различных значениях параметра нагружения .
Математически можно предложить следующую модель нелинейного осциллятора:
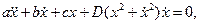
где можно принять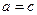 
, 
, 
, 
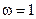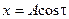. Параметр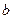 
может быть равен: 
.
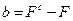Случай положительных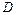 
представляет динамический аналог устойчиво симметричной точки бифуркации. Тривиальное состояние 
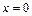является устойчивым для 
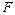, меньших 
, и представляет притягивающий фокус. Для 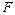, больших , это состояние соответствует неустойчивому отталкивающему фокусу, и все локальные движения системы стремятся к устойчивому притягивающему предельному циклу, представляющему устойчивое конечное колебание. Амплитуда предельного цикла увеличивается с ростом 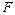от значения, равного нулю в критическом равновесном состоянии (рисунок 1.68).
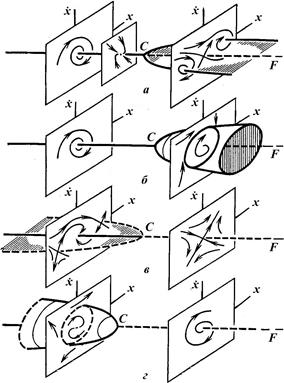
Рисунок 1.68 - Сравнение двух статических и динамических бифуркаций:
а – статически устойчивая бифуркация; б – динамически устойчивая бифуркация; в – статически неустойчивая бифуркация; г – динамически неустойчивая бифуркация
Динамический аналог неустойчиво симметричной точки бифуркации соответствует случаю, когда коэффициент нелинейности 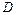отрицателен.
Тривиальное равновесное решение опять теряет свою устойчивость при 
. При этом значении притягивающий фокус переходит в отталкивающий.
Устойчивое до критическое равновесное состояние имеет лишь конечную область притяжения, ограниченную неустойчивым предельным циклом. Если в результате конечного возмущения система оказалась вне этого цикла, то возникнут возрастающие колебания, даже если управляющий параметр 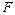меньше своего критического значения. Устойчивое тривиальное решение при этом называют метаустойчивым, как в соответствующей статической неустойчиво симметричной бифуркации. Наиболее типичные динамические бифуркации такого типа называют бифуркациями Хопфа после появления знаменитой теоремы.
Наглядно изобразить перестройки в фазовом пространстве для четырех симметричных бифуркаций на одной диаграмме, как сделано на рисунка. Здесь фазовые портреты воспроизведены для до- и за критической нагрузок и хорошо видны аналогии между двумя статическими и динамическими бифуркациями.
Для двух статических бифуркаций фокус всегда переходит в узел в окрестности бифуркации – это не во всех случаях специально оговаривается.
В гидродинамике устойчиво (неустойчиво) симметричные бифуркации называются за(до)критическими бифуркациями, и топологи по очевидным соображениям называют симметричную бифуркацию камертоном. Асимметричную точку бифуркации называют транскритической бифуркацией.
Мы вернемся к динамическим бифуркациям позже при обсуждении гидростатических нагрузок на сооружения, а теперь обратимся к более тщательному рассмотрению статических бифуркаций, типичных для поведения консервативных систем.
