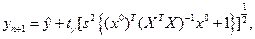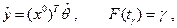Перспективным направлением организации технического обслуживания является эксплуатация систем по состоянию, которая предполагает периодический контроль и измерение параметров, определяющих техническое состояние изделий. При этом решение о замене или восстановлении работоспособности изделия принимается тогда, когда значение параметров работоспособности достигают критического уровня соответствующего отказу.
Для анализа предлагаемого подхода проанализируем возможные реализации монотонно возрастающего случайного процесса. Очевидно, достижение допустимого уровня приводит к отказу устройства. Следовательно останавливать наблюдение и проводить замену необходимо до достижения критического уровня. В дальнейшем решим задачу отыскания оптимального момента замены системы по информации о поведении конкретной реализации процесса. Допустим, что после проведения «i» наблюдений известно, что изделие находится в работоспособном состоянии. Для решения вопроса о целесообразности его замены нужно оценить работоспособность системы на (i + 1) – ом шаге ее функционирования.
Таким образом возникает задача прогнозирования поведения случайного процесса y(t) на (i +1) – ом шаге по результатам измерений в предшествующие моменты времени. Существуют различные методы прогнозирования случайных процессов.
В дальнейшем остановимся на методе наименьших квадратов, нашедшем широкое применение в инженерной практике.
При решении задачи будем предполагать, что случайная функция может быть представлена в виде
или в матричной форме
(4.30)
где 
- вектор значений функции;
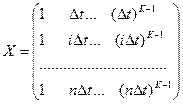- матрица известных координат;
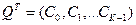- вектор неизвестных параметров;
n – число измерений;
K – число неизвестных параметров.
С учетом случайных воздействий уравнение (4.30) примет вид
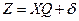
где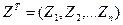 
- вектор измерений;
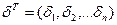- вектор случайных воздействий.
Согласно методу наименьших квадратов оценки неизвестных параметров 
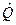удовлетворяют соотношению
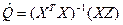
Точность оценок определяется дисперсионной матрицей
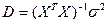
где 
- дисперсия случайных воздействий 
.
При отсутствии априорной информации о статистических свойствах случайных воздействий, неизвестную дисперсию можно оценить по соотношению
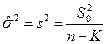
где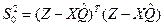 
- остаточная сумма квадратов.
Очевидно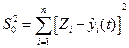 
Полученные результаты позволяют оценить верхнюю границу доверительного интервала, соответствующего, прогнозируемому на (n+1)–ом шаге, значению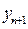 
. Верхняя граница доверительного интервала для 
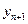оценивается по соотношению
где 
