Стратегия технического обслуживания по гарантированному ресурсу

Очевидно использование стратегии аварийных замен неприемлемо для тех ситуаций, когда отказ системы приводит к катастрофическим последствиям.

В этих случаях назначают гарантированный ресурс. Согласно ГОСТ 27.002-83 вводится понятие гамма-процентного ресурса, который характеризует наработку, в течении которой объект не достигнет предельного состояния с заданной вероятностью , выраженной в процентах. Величину гамма-процентного ресурса можно определить по соотношению

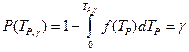
где - вероятность обеспечения ресурса , соответствующего заданному уровню доверительной вероятности ,

- наработка до предельного состояния.

Процесс приближения технического объекта к отказам удобно характеризовать движением случайно изменяющегося в течение времени эксплуатации векторного параметра работоспособности ПР объекта к границе рабочей области, при достижении которой определяющим параметром объект теряет работоспособность. По числовым характеристикам этого процесса имеется принципиальная возможность найти распределение наработки до отказа объекта и ее характерную точку — время сохранения работоспособности. Далее для простоты будем рассматривать только случайный процесс изменения во времени одной координаты ПР, не забывая, однако, что при необходимости полученные при этом результаты распространяются на случай приближения векторного ПР к границе многомерной рабочей области.

Основой случайных процессов изменения ПР являются необратимые случайные изменения, вызванные старением, износом или разрегулированием и имеющие определенную зависимость от времени. При этом случайный характер таких изменений обусловлен случайными параметрами, не зависящими от времени. Следовательно, модели реального изменения ПР объекта также должны принадлежать к классу случайных функций, аргументами которых являются постоянные во времени случайные величины и само время. Наиболее простые функции, удовлетворяющие этому условию, — линейные случайные функции. При линеаризации реального процесса износа, старения или разрегулирования объекта каждая реализация процесса заменяется прямой, т. е. реальный процесс изменения ПР X(t) аппроксимируется случайной функцией Х₁(t):

Х₁(t) = X₀±Vt

где Х₀ —начальное значение ПР (при t=0), V — случайная нормально распределенная скорость изменения ПР во времени.

Распределение наработки до отказа находят по правилам определения законов распределения функций случайных аргументов, в частности закона распределения монотонной функции одного случайного аргумента. Правила заключаются в следующем. Если имеется непрерывная случайная величина х с плотностью распределения f(x), а другая случайная величина t связана с нею функциональной зависимостью t=φ(x), то плотность распределения случайной величины t определяется соотношением[16]

g(t) = f(ψ(t)) | ψ^/(t) |

где ψ — функция, обратная функции φ

Рассмотрим это правило применительно к первому варианту.

Пусть определяющий параметр изменяется (например, увеличивается) линейно во времени

x(t) = x₀+Vt

где x₀ и V — начальное значение и скорость, изменения во времени определяющего параметра.

При этом начальное значение параметра практически постоянно (х₀==соnst), а скорость изменения определяющего параметра во времени, будучи постоянной в каждой конкретной реализации, от реализации к реализации меняется случайным образом, в частности по нормальному закону:

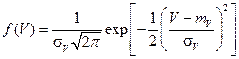
где т_V, σ_V — МОЖ и среднеквадратическое отклонение скорости изменения во времени параметра x. Рассматриваемый случай представлен на рис.4.4а.

x_m

X₀

Рис 4.4а. График веерной функции x(t)

При этом случайная величина наработки t до отказа связана с начальным и предельным значениями, а также со случайной скоростью V изменения во времени параметра х следующей функциональной зависимостью:

t = Δx/V, (4.21)

где Δx = (x_m-x₀) — детерминированная величина, характеризующая запас работоспособности (долговечности) по параметру х.

С учетом соотношения (4.21) имеем

Ψ(t) = Δx/t

В свою очередь, из этого выражения следует

| Ψ΄(t)| = Δx/t²

После подстановки получим:

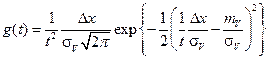(4.22)

Обозначим:

(4.23)

На основании соотношения (4.22) с учетом зависимостей (4.23) получаем

(4.24)

где

β₀=Δx/σ_V

α₀=m_V/σ_V

Соотношение (4.24) определяет плотность альфа - распределения наработки до отказа.

При этом параметр β₀, имеющий размерность наработки, принято называть относительным запасом работоспособности (долговечности) по параметру х, а параметр α₀ называют относительной средней скоростью изменения параметра х или коэффициентом однородности скорости, изменениям параметра х.

Математическое ожидание и среднеквадратическое отклонение наработки до отказа находятся в известной функциональной зависимости от плотности распределения наработки до отказа:

;

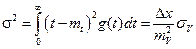В дальнейшем предположим, что определяющий параметр изменяется по экспоненциальному закону

, где , а V – подчиняется нормальному закону.

Логарифмируя, получим .

Вводя обозначения: , приходим к линейной зависимости

Следовательно для рассматриваемого случая можно воспользоваться результатами, полученными ранее для веерной функции. Для иллюстрации рассмотрим пример оценки надежности трубопровода с учетом коррозии. В общем случае закон снижения толщины трубы при воздействии коррозии можно оценить по соотношению ,

где случайная скорость изменения радиуса трубы в течении ее эксплуатации.

Изменение работоспособной толщины трубы в процессе эксплуатации представлено на рис.4.4в

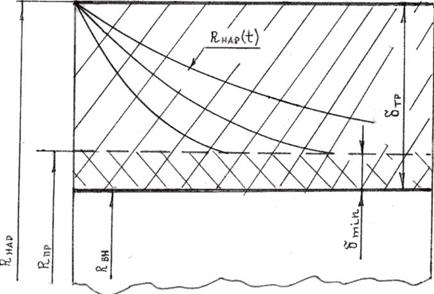
Рис.4.4в Расчетная схема функционирования трубопровода. с учетом старения.

На рисунке введены следующие обозначения: 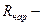начальный наружный радиус трубы;

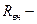внутренний радиус трубы; предельное значение внешнего радиуса;

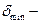минимальная толщина трубы, обеспечивающая ее работоспособность.

В рассматриваемом случае среднее время до отказа трубопровода будет равно

, (4.25) где - запас работоспособности трубы; 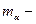математическое ожидание скорости коррозии

В дальнейшем допустим, что потребное среднее время до отказа будет равно , где k- степень увеличения среднего времени до отказа по сравнению с существующим уровнем. С учетом (4.25) соотношение примет вид . С другой стороны имеем

, где .

Следовательно . Таким образом справедливо соотношение .

Производя преобразования, получим

Отсюда .

В частности при получим .

Таким образом для увеличения среднего времени до отказа в три раза потребуется удвоить толщину стенки трубопровода.

Рассмотрим еще один способ определения распределения наработки до отказа 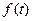через одномерные характеристики плотности распределения f(η,t) случайной функции η(t) и характеристики поля допуска при следующих ограничениях: закон распределения f(η,t) в вертикальных сечениях во времени не изменяется; реализация η(t) и моментные функции ξ(t) случайного процесса η(t) во времени изменяются монотонно; в начальный момент времени t₀ значения параметра находятся в границах поля допуска, т.е.P{a<η<b,t₀}=1

Принятые предположения вполне согласуются с имеющимися представлениями о процессах накопления повреждений узлами и деталями механических систем, подверженными износу и старению, а точность полученных результатов будет зависеть от того, насколько эти предпосылки близки к реальным. При указанных предположениях связь φ(t) c f(η,t) при двустороннем поле допуска (а,b) определяется следующим выражением[16]:

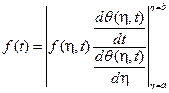где η=b, η=a означает, что после дифференцирования необходимо написать разность полученных результатов и в первом члене разности поставить вместо η значения верхней границы поля допусков η=b, а во втором — значения нижней границы η=a, θ(η,t) — функция, которая представляет собой последнюю общую ступень дифференцирования F(η,t) до η и t.

Для нормального закона распределения η при двустороннем допуске (а, b):

(4.26)

где

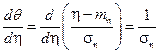
а при одностороннем допуске c

(4.27)

Пример.

Примем

где с>0 (неслучайная величина)

Получим

(4.28)

В случае линейной зависимости (с=1) приходим к известным распределениям (см. таблицу 4.4).

Таблица 4.4

Параметр	Вид распределения
С=1 D₀=0	α – распределение 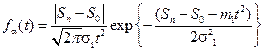где S₀ – детерминированное S₁=N{m₁,σ₁}
C=1	Распределение Бернштейна где

В заключении приведем вывод соотношения (4.28).

В рассматриваемом случае

Отсюда

Соответственно

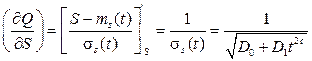
Таким образом

где

После преобразований получим

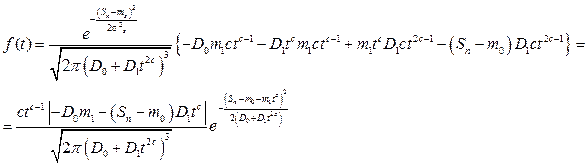(4.29)

Знание закона распределения наработки позволяет находить величину гарантированного ресурса для любого заданного значения доверительной вероятности . Очевидно при катастрофических последствиях отказа, величина должна назначаться из соображений обеспечения безопасности. Если отказ сводится только к материальному ущербу, ресурс системы целесообразно задавать из условия минимизации суммарных затрат на ее эксплуатацию. Более подробно эта задача рассматривается в следующих разделах работы.