При решении задачи нормирования в качестве целевой функции примем суммарные затраты на реализацию целевой программы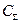 
.
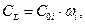
| (1.79) |
где 
- стоимость нерезервированной i -ой системы;
- кратность резерва i -ой системы.
С учетом введения «горячего» резерва вероятность отказа i -ой системы будет равна
|
где 
- вероятность отказа нерезервированной i -ой системы.
В качестве дисциплинирующего условия рассмотрим обеспечение заданного уровня показателя эффективности
| (1.80) |
Для решения задачи воспользуемся методом неопределенных множителей Лагранжа. Функция Лагранжа будет равна
|
где 
.
Оптимальное решение должно удовлетворять системе алгебраических уравнений
 
|
Производя дифференцирование, получим
|
Решая уравнение относительно 
, получим
|
где 
Подставляя выражение для 
в дисциплинирующее условие (1.80) будем иметь
|
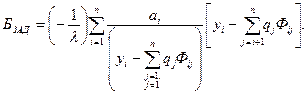
Отсюда
|
Таким образом, окончательно получим
| (1.81) |
Заметим, что в случае, когда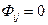 
, соотношение для упростится
|
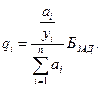
Значение позволяет оценить оптимальную кратность резерва по соотношению
|
