В предположении нормального закона распределения коэффициента запаса η соотношение (2.13) примет вид
(2.14)
где mη – математическое ожидание коэффициента запаса;
ση – среднеквадратическое отклонение коэффициента запаса.
Для оценки mη и ση воспользуемся методом линеаризации. Разлагая функцию η в ряд Тейлора в окрестности математического ожидания аргументов и ограничиваясь линейными членами, получим
mη = mхдог / mхд,
где mхд, mхдог – соответственно математические ожидания действующих и допустимых значений параметров;
σхд, σхдоп – соответственно средние квадратические отклонения действующих и допустимых значений параметров.
Индекс «m» в выражении для ση означает, что частные производные берутся в точке математического ожидания аргументов.
После преобразований выражение для ση представим в виде
где
- соответственно коэффициенты вариации действующих и допустимых значений параметров.
Подставляя выражение для ση в соотношение (2.14), получим
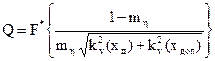
Таким образом, для оценки вероятности отказа по каждому параметру необходимо знание коэффициентов вариации действующих и допустимых значений параметров и коэффициента запаса η.
При проведении анализа будем считать известными значения коэффициентов вариации по каждому из рассматриваемых параметров. Введение этого допущения не снижает практической ценности исследования. Действительно, коэффициенты вариации обладают свойством стабильности и поэтому их значения могут быть рассчитаны по статистическим данным, полученным ранее для аналогичных изделий.
Величину коэффициента запаса будем оценивать по результатам проведения испытаний. В дальнейшем будем предполагать, что в процессе каждого i –го испытания производится измерение действующих хдi и допустимых хдопi значений параметров. По результатам измерений можно рассчитать значения коэффициента запаса
Таким образом, после проведения испытаний для каждого параметра получим выборку значений η1, η2, …,ηк. По выборке значений ηi, используя известные методы математической статистики, найдем оценку математического ожидания коэффициента запаса
 |
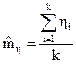(2.15)
Математическое ожидание этой оценки равно истинному значению, то есть М{mη} = mη. Среднеквадратическое отклонение оценки (2.15) может быть рассчитано по соотношению
 |
Знание позволяет получить точечную оценку вероятности отказа
(2.16
 | |||
| |||
Очевидно, величина, а следовательно, и, будут случайными. Поэтому для получения гарантированного результата необходимо перейти к интервальной оценке. С этой целью определим односторонние верхние и нижние границы надежности. Верхняя граница доверительного интервала определяется по соотношению
Р{H < НВ} = γ (2.17)
где γ – уровень доверительной вероятности. Соотношение (2.17) показывает, что с вероятностью γ истинное значение надежности H лежит левее верхней границы НВ.
Соответственно для нижней границы интервала НВ, имеем
Р{H > НН} = γ (2.18)
Соотношение (2.18) показывает, что с вероятностью γ истинное значение надежности H лежит правее нижней границы НН.
Тогда, если Hзад < НН, то испытания следует прекратить, так как с вероятностью γ истинное значение надежности будет больше НН, а, следовательно, и Hзад. Если Hзад > НВ, то следует проводить доработку, так как истинное значение надежности с вероятностью γ будет меньше НВ, а, следовательно, и Hзад. Если Hзад лежит внутри интервала (НВ,НН), то истинное значение надежности может быть как больше, так и меньше Hзад и никакого заключения сделать нельзя, то есть испытания следует продолжить.
Ввиду монотонности функции нормированного нормального распределения выражение для односторонних верхней и нижней границ можно представить в виде
где ηН, ηВ - соответственно односторонняя нижняя и верхняя границы доверительного интервала для коэффициента запаса.
Границы доверительного интервала по η можно приближенно представить в виде
(2.19)
где tγ – квантиль, соответствующий принятому уровню доверительной вероятности γ.
С учетом соотношения (2.16), получим
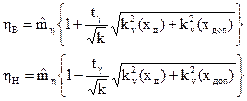
(2.20)
Приравнивая выражения для верхней и нижней границ заданному значению коэффициента запаса и разрешая полученные соотношения относительно, получим выражения для верхней и нижней граничных кривых, определяющих области отработки изделия
(2.21)
|
Граничные кривые (2..21) разбивают все пространство значений на три области: область прекращения отработки, область продолжения испытаний и область доработок (рис. 2.5). На графике представлены возможные реализации траекторий (К), полученные по результатам проведения конкретных испытаний. Для построения кривых (К) значения должны рассчитываться после проведения каждого испытания. Пересечения кривых mη (К) с границами определяют момент окончания испытаний (К1 – прекращение испытаний в связи с подтверждением надежности, К2 - прекращение испытаний для проведения доработки). Фактически точка К2 характеризует момент обнаружения неисправности. Использование предложенного подхода позволяет существенно сократить количество испытаний для устранения предполагаемых источников отказа. В частности, появляется возможность обнаруживать источник отказа даже при положительных реализациях функции работоспособности, то есть при отсутствии фактических отказов изделия.
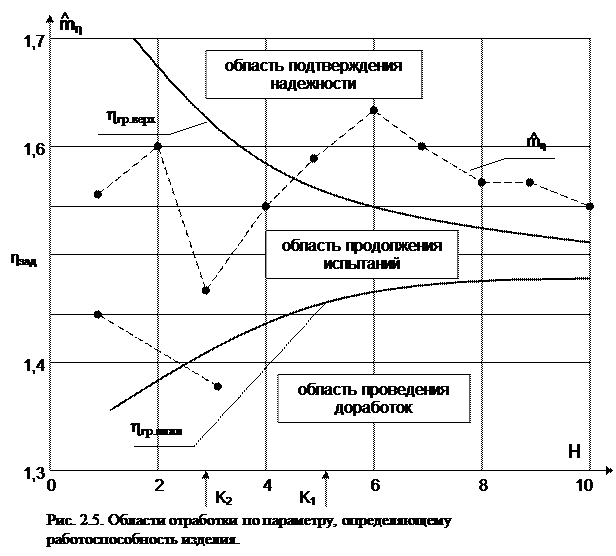Полученные результаты позволяют проанализировать влияние резервирования на продолжительность экспериментальной отработки. При схемном резервировании требование к надежности устройства падает, что приводит к снижению верхней границы ηгр.верх и подтверждению надежности при меньшем числе испытаний. При параметрическом резервировании кривая пойдет выше и пересечение верхней границы ηгр.верх произойдет раньше.
Таким образом, введение соответствующих уровней избыточности позволяет обеспечить требования по надежности изделия для любого заданного объема испытаний, что особенно важно, когда заданы жесткие ограничения на время отработки изделия.
Для иллюстрации метода рассмотрим конкретный пример. Допустим проведено 2 испытания, в результате обработки которых получено значение = 2.
Тогда при Кv(хд) = 0,1 и Кv(хдоп) = 0,1 точечная оценка надежности будет равна
 |
(2.22)
Гарантированная оценка надежности НН с уровнем доверия γ = 0,95 (tγ = 1,65) будет равна
(2.23)
Для нашего случая получим
Заметим, что для подтверждения такого уровня надежности при проведении испытаний по схеме «да – нет» потребовалось бы 1000 испытаний. В заключение отметим, что полученное решение является приближенным. Тем не менее, оно позволяет достаточно просто рассчитывать границы доверительного интервала с требуемой для инженерных расчетов степенью точности.
Для реализации предложенного подхода достаточно по выборке значений параметров работоспособности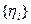 
оценить среднее значение параметра 
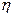по соотношению (2.15) и для принятого уровня доверия 
рассчитать нижнюю границу надежности 
по соотношению (2.23).
Выборка 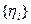может быть сформирована по результатам испытаний, проводимых в процессе ЭО двигателя. Например, в ходе испытаний двигателя замеряют температуру и давление в камере сгорания, давление наддува в баках окислителя и горючего, давление в топливных магистралях, уровни компонентов по показаниям датчиков СОБ, число оборотов турбины, тягу двигателя, перегрузки и др. параметры. Знание этих параметров позволяет сформировать выборки значений коэффициентов запаса по различным предельным состояниям. В частности, для обеспечения бескавитационной работы насоса необходимо выполнение условия
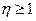
где 
, 
, 
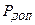- действующее и допустимое давления на входе в насос. Величина является случайной. Зная реализации значений 
можно рассчитать соответствующие значения коэффициентов запаса, получить выборку 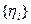и оценить параметрическую надежность.
Как было показано выше измерение параметров работоспособности позволяет подтверждать высокие уровни надежности изделия Однако, для ряда агрегатов и систем ДУ проведение измерений в процессе испытаний оказывается затруднительным. Например, такой подход оказывается неприемлемым для изделий однократного действия, единственным признаком безотказности которых служит факт их срабатывания (воспламенителей, пирозамков, разрывных мембран и др.) Для них экспериментальная отработка проводится по схеме «успех-отказ», дающий информацию только об успешном или неуспешном окончании испытаний. В этом случае задача сокращения количества испытаний может быть решена путем проведения утяжеленных испытаний. Согласно методу утяжеленных испытаний отработку изделия производят при более тяжелых, по сравнению со штатным, режимах работы. По результатам утяжеленных испытаний производится оценка надежности системы, которая затем соответствующим перерасчетом приводится в соответствии со штатным режимом ее функционирования. Отметим, что проведение утяжеленных испытаний предполагает наличие избыточности системы по параметрам, характеризующим ее работоспособность. Очевидно, более высокие уровни избыточности, закладываемые на этапе проектирования, позволяют реализовывать более тяжелые режимы испытаний, а, следовательно, проводить отработку при меньшем числе испытаний. В дальнейшем при изложении метода примем допущение о нормальности функции распределения параметра 
Очевидно, при проведении утяжеленных испытаний коэффициент запаса 
будет меньше, чем при штатном функционировании. Далее предположим, что значения и 
могут быть выражены друг через друга через коэффициент утяжеления
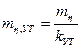
Величина 
определяется исходя из условий функционирования изделия в штатном и утяжеленном режимах.
После проведения утяжеленных испытаний по таблицам оценивается нижняя граница доверительного интервала надежности 
при принятом уровне доверия 
Знание 
позволяет определить соответсвующее ей значение 
Далее определяем значение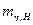 
, соответствующее штатному режиму работы системы
Знание 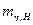позволяет оценить надежность по соотношению
Для иллюстрации рассмотрим численный пример. Допустим для рассматриваемого случая относительные разбросы параметра работоспособности будут равны
Утяжеленные испытания проводились с коэффициентом 
. При десяти испытаниях произошел один отказ. Задаваясь 
, по таблицам [18 ]
находим: 
. Подставляя исходные данные в расчетное соотношение, получим
.
Отсюда
2 0,966 = 1,932.
Таким образом, имеем
.
Заметим, что для подтверждения такого же уровня при испытаниях типа
«успех-отказ» потребовалось бы порядка десяти тысяч безотказных испытаний.
