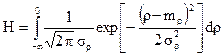 Величина Н может быть вычислена по соотношению (2.22), если известен конкретный вид плотности распределения f(ρ). Для нормального закона распределения соотношение (1.22) примет вид
Величина Н может быть вычислена по соотношению (2.22), если известен конкретный вид плотности распределения f(ρ). Для нормального закона распределения соотношение (1.22) примет вид
(1.23)
К сожалению, интеграл (1.23) не выражается аналитически и его для каждого конкретного случая надо вычислять численно. Чтобы упростить расчеты, целесообразно перейти к нормированным случайным величинам u, имеющим нулевое математическое ожидание и единичную дисперсию. Этот переход может быть осуществлен с помощью следующих эквивалентных преобразований
 |
(1.24)
 |
Отсюда
(1.25)
где V = - mρ / σρ, F*{V} – функция нормированного нормального распределения. Интеграл (1.25), задающий функцию F*{V}, тоже не берущийся, однако, он не зависит только от одного параметра V. Значения функции F*{V} для разных V подсчитаны численным методом и сведены в табл. 1.2.. Таким образом, при оценке надежности достаточно вычислить параметр V= -mρ/σρ и определить по таблице [18] соответствующую величину функции F*{V}.
Функция нормированного нормального распределения
Таблица 1.2

Для нахождения  и
и 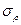 наиболее удобно воспользоваться методом линеаризации
наиболее удобно воспользоваться методом линеаризации

где  ;
; 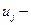 случайные величины, определяющие случайный характер функции работоспособности.
случайные величины, определяющие случайный характер функции работоспособности.
В дальнейшем условие работоспособности по каждому из параметров представим в виде неравенства
η > 1,
где η = хдоп / хд – коэффициент запаса по рассматриваемому параметру;
хд, хдоп – соответственно действующее и допустимое значение параметра.
Тогда вероятность отказа по данному параметру можно представить в виде
Q = Р{η < 1}
 В предположении нормального закона распределения коэффициента запаса η, получим
В предположении нормального закона распределения коэффициента запаса η, получим
где mη – математическое ожидание коэффициента запаса;
ση – среднеквадратическое отклонение коэффициента запаса.
Для оценки mη и ση воспользуемся методом линеаризации. Разлагая функцию η в ряд Тейлора в окрестности математического ожидания аргументов и ограничиваясь линейными членами, получим

mη = mхдог / mхд,
где mхд, mхдог – соответственно математические ожидания действующих и допустимых значений параметров;
σхд, σхдоп – соответственно средние квадратические отклонения действующих и допустимых значений параметров.
Индекс «m» в выражении для ση означает, что частные производные берутся в точке математического ожидания аргументов.
После преобразований выражение для ση представим в виде

 где
где
- соответственно коэффициенты вариации
действующих и допустимых значений параметров.
Подставляя выражение для ση в соотношение для Q, получим
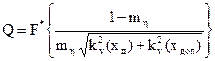
Таким образом, для оценки вероятности отказа по каждому параметру необходимо знание коэффициентов вариации действующих и допустимых значений параметров и коэффициента запаса η При проведении анализа будем считать известными значения коэффициентов вариации по каждому из рассматриваемых параметров. Введение этого допущения не снижает практической ценности исследования. Действительно, коэффициенты вариации обладают свойством стабильности и поэтому их значения могут быть рассчитаны по статистическим данным, полученным ранее для аналогичных изделий.
В дальнейшем рассмотрим задачу оценки  для функций различного вида. Сначала рассмотрим аддитивную функцию двух переменных. Пусть
для функций различного вида. Сначала рассмотрим аддитивную функцию двух переменных. Пусть
 ,
,
где  и
и  независимые, положительно определенные случайные величины.
независимые, положительно определенные случайные величины.
Для данного случая имеем

Выражения удобней представить в виде
 .
.
Далее предполагая, что отношение  , можно получить следующую оценку
, можно получить следующую оценку

Отсюда 
Аналогично в предположении, что  , получим
, получим  .
.
Таким образом в общем случае можно записать  .
.
Эта оценка может быть уточнена, если известен вклад каждого из слагаемых в суммарную функцию  . Предполагая независимость
. Предполагая независимость  , получим
, получим
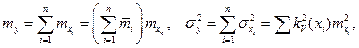
где  относительный вклад i-го слагаемого;
относительный вклад i-го слагаемого;
 математическое ожидание и дисперсия i-го параметра;
математическое ожидание и дисперсия i-го параметра;
 коэффициент вариации i-го параметра.
коэффициент вариации i-го параметра.
Тогда
 .
.
В дальнейшем рассмотрим функцию равную произведению двух переменных:  .
.
.Производя линеаризацию функции y в окрестности математических ожиданий случайных величин  и
и  получим
получим
 .
.
Тогда выражения для  и
и 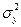 примут вид
примут вид
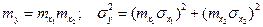 .
.
Отсюда найдем  .
.
Аналогично можно показать, что оценка остается справедливой и для случая, когда y является отношением двух независимых случайных величин  .
.
Нетрудно заметить, что полученные выше формулы путем последовательной группировки слагаемых (или сомножителей) легко обобщить на случай трех и более переменных. Так для функции  формула для
формула для 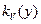 примет вид
примет вид

Аналогично для функции  имеем
имеем

Более того методом последовательной группировки можно находить искомые оценки коэффициента вариации для различных комбинаций исходных параметров. Так для функции вида  получим
получим

В заключение найдем оценку коэффициента вариации для функции одной переменной
 . Используя метод линеаризации и производя выкладки, аналогичные предыдущим, получим
. Используя метод линеаризации и производя выкладки, аналогичные предыдущим, получим

В частности для функции  получим
получим  .
.






