Уменьшить случайную погрешность можно, определяя оценку математического ожидания многократных наблюдений измеряемой величины Х. В этом случае за результат измерения, как правило, принимается среднее арифметическое результатов наблюдений
.
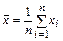Поскольку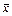 
определяется по конечному числу наблюдений, то является случайной величиной.
Дисперсия среднего арифметического результатов наблюдений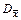 
в n раз меньше дисперсии однократного наблюдения 
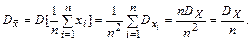
Поэтому, принимая за результат измерения 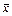, можно ожидать уменьшения случайной погрешности.
Границы погрешности среднего арифметического будут, очевидно, определяться выражением
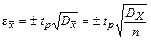. (2.47)
Для определения границ погрешности среднего арифметического необходимо знать его закон распределения.
Центральная предельная теорема теории вероятности гласит: если имеется n независимых случайных величин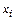 
распределенных по одному и тому же закону с математическим ожиданием 
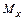и дисперсией , то при неограниченном увеличении n закон распределения суммы 
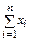неограниченно приближается к нормальному. Считается, что при n > 20…30 центральная предельная теорема соблюдается, поэтому в этом случае значения доверительного коэффициента в выражении (2.47) берется из таблицы для нормального распределения.
Если n < 20…30, то распределение 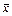уже нельзя считать нормальным. Как же определить 
для этого случая?
Доверительная вероятность для 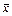равна
.
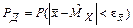Деля обе части неравенства на
,
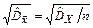получаем
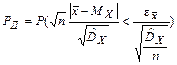. (2.48)
Обозначим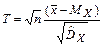 
, тогда
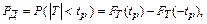
где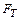 
- интегральная функция распределения величины Т.
Закон распределения Т зависит от закона распределения 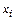и числа наблюдений n.
Из теории вероятности известно, что если величина 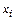распределена по нормальному закону, то величина Т распределена по так называемому закону Стьюдента с k = (n -1) степенью свободы.
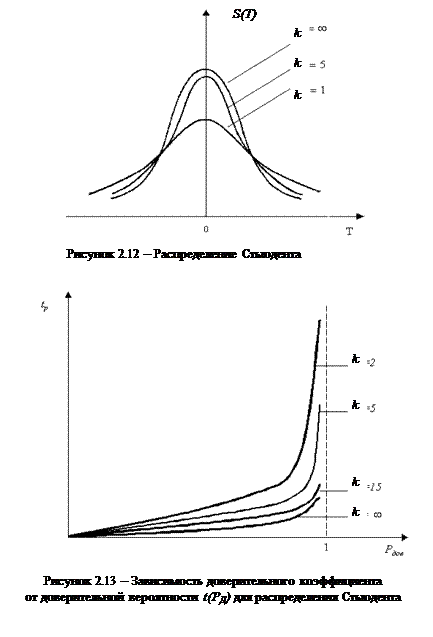
Плотность распределения Стьюдента имеет вид (рис.2.12)
.
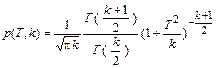С ростом n распределения Стьюдента приближается к нормальному и при n >20…30 уже неотличимо от него (рис 2.13).
Таким образом, если известно, что результаты отдельных наблюдений распределены по нормальному закону, то при числе наблюдений n =2…20 при определении границ случайной погрешности доверительный коэффициент берется из таблиц распределения Стьюдента для (n -1)-й степени свободы и заданной доверительной вероятности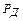 
. Зависимость коэффициента Стьюдента 
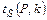приведена на рис. 2.13 и в табл. А5.
При отсутствии таблиц с распределением Стьюдента, значение коэффициента 
для n =6…20 можно определить приближенно (с погрешностью до 20%) по формуле
,
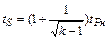где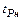 
- доверительный коэффициент для нормального распределения.
Более точно (с погрешностью не более 5%) значение коэффициента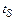 
для n > 4 и 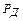> 0,9 можно аппроксимировать выражением
 |
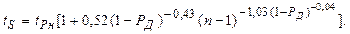
2.4 Грубые погрешности и промахи
Грубые погрешности и промахи являются особым видом случайных погрешностей. Грубые погрешности вызваны, как правило, резкими кратковременными изменениями условий измерений: механическими толчками, вибрациями, колебаниями внешних условий, скачками питающего напряжения. Промахи относятся к личным погрешностям и обусловлены неправильными действиями оператора (некорректное считывание показаний прибора, неправильной их записью и т.п.) И те, и другие погрешности вызывают заметные отличия в результатах наблюдений. Такие “подозрительные” результаты не подчиняются закону распределения основной массы результатов наблюдений и должны быть устранены из их числа.
Обнаружение грубых погрешностей и промахов производится с помощью специальных критериев, основанных на аппарате математической статистики.
