Плотность распределения
Так как в выражение для функции распределения не входит аргумент X, то обычная техника использования принципа максимального правдоподобия здесь неприемлема. Однако в этом случае экстремальная задача может быть решена непосредственно.
Функция правдоподобия
.
Параметры a и b отыскиваются из ряда наблюдений 
,причем
;
.
Очевидно, что решение экстремальной задачи 
будет достигаться в том случае, когда
,
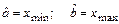т.е. для равномерного распределения эффективные оценки математического ожидания и дисперсии будут находиться через минимальные и максимальные значения ряда наблюдений. Поэтому эффективной оценкой математического ожидания является полуразмах
, (2.42) 
а дисперсия
. (2.43)
Для других симметричных распределений предлагается определять эффективную оценку математического ожидания в зависимости от величины оценки островершинности (эксцесса) их распределений
- 3.
Если 
т.е. распределение близко к экспоненциальному (Е =3), то за оценку математического ожидания лучше взять медиану.
Если - 
, т.е. распределение близко к нормальному (
), то за ее оценку лучше взять среднее арифметическое.
Если Е <-0,5, т.е. распределение близко к равномерному, то наиболее целесообразно оценкой математического ожидания считать полуразмах. Эффективные оценки дисперсии в этих случаях соответствуют эффективным оценкам дисперсии указанных распределений (табл.2.2).
Таблица 2.2 - Эффективные оценки математического ожидания и СК0 симметричных распределений
| Е | < -0,5 | -0,5...1 | >1 |
| 
| 
| 
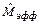
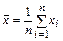
Смотри (2.39)
|
| 
| 
| 
|
