Результат измерения 
(
или 
) не принадлежит заданному распределению (т.е. отягощен грубой погрешностью или промахом) с заданной вероятностью Р, если
, (2.52)
где 
- доверительный коэффициент или, другими словами, если выходит за границы интервала 
.
Для нормального распределения обычно выбирают Р = 0,9973, для которого 
, поэтому в этом случае критерий известен под названием “правило 3-х сигм”. Вероятность отклонения “нормального" результата наблюдения за указанные границы в этом случае равна малой величине 
.
Аналогичным образом можно сформулировать данный критерий и для других распределений. Для распределений, обладающих, в отличие от нормального, границами, следует выбирать Р =1.
В этом случае вероятность появления результатов наблюдения за границами распределения равна нулю. Значения 
, при Р =1 для разных распределений указаны в таблице 2.4.
Таблица 2.4 - Значения для различных распределений
| Вид распределения | Аркси-нуса | Равно-мерное | Симп-сона | Норма-льное | Лапласа |
|
| 
| 
| 
|
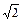
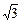
Недостаток критерия - он справедлив для количества наблюдений n >20…30, для которого можно считать, что 
и 
.
