Свойство полноты информации негласно предполагает, что имеется возможность измерять количество информации. Какое количество информации содержится в данной лекции, какое количество информации в популярной песенке? Ответы на подобные вопросы не просты и не однозначны, так как во всякой информации присутствует субъективная компонента.
Информационные сообщения могут рассматриваться на трёх уровнях. На синтаксическом уровне рассматриваются только данные как последовательности символов. На семантическом – анализируется смысловое содержание сообщения по отношению к источнику. На прагматическом – рассматривается потребительская ценность сообщения – отношение к получателю.
Самый простой способ измерения информации – объёмный – это количество символов в сообщении. Этот способ чувствителен к форме представления сообщения, так как, например, одно и то же число может записываться по-разному с использованием разных алфавитов: «восемь», 8, VIII или 1000 – в двоичной форме.
При энтропийном подходе количеством информации называют числовую характеристику информации, отражающую ту степень неопределённости, которая исчезает после получения информации. Так, бросание монеты может привести к одному из двух равновероятных состояний: орёл или решка. В результате броска неопределённость снимается. При числе равновероятных состояний N количество информации Н определяется по формуле Хартли:
Н =log2 N. (1.1)
Для неравновероятных состояний используется формула Шеннона:
(1.2)
где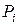 
– вероятность появления i -го символа.
За единицу информации принимается один бит (англ. bit – binary digit – двоичная цифра). Это количество информации, при котором неопределённость, т.е. количество вариантов выбора, уменьшается вдвое или, другими словами, это ответ на вопрос, требующий односложного разрешения – да или нет. За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных состояний. Это будет не двоичная (бит), а десятичная (дит) единица информации. Для получения количества информации в дитах следует заменить логарифм по основанию 2 десятичным логарифмом. По аналогии, используя натуральный логарифм, можно определить количество информации в натах.
Бит – минимальная единица измерения информации. На практике чаще применяются более крупные единицы, например, байт, являющийся последовательностью из восьми бит. Именно восемь битов, или один байт, используется для того, чтобы закодировать символы алфавита, клавиши клавиатуры компьютера. Один байт также является минимальной единицей адресуемой памяти компьютера, т.е. обратиться в память можно к байту, а не биту.
Широко используются ещё более крупные производные единицы информации:
1 Килобайт (Кбайт) = 1024 байт = 210 байт = 213 бит,
1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт = 223 бит,
1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт = 233 бит,
1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт = 243 бит.
