Зависимости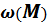 
или 
( 
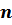) называются механическими характеристиками.
Механические характеристики исполнительных механизмов – это зависимости между приведенными к валу двигателя скоростью и статическим моментом (моментом сопротивления) механизма.
Для правильного проектирования и экономичной эксплуатации электропиривода необходимо соответствие механических характеристик двигателя и характеристик исполнительных механизмов.
В отличие от двигателей значение статического момента (момента сопротивления) механизма зависит от скорости рабочего органа. И механические характеристики исполнительных механизмов в технической документации представляют функцией статического момента – 
от угловой скорости – ω, т.е
= f (ω). (4-4)
Но для удобства совместного рассмотрения механических характеристик электродвигателя и механизма, характеристику исполнительного механизма изображают как функцию скорости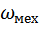 
, приведенной к валу двигателя от статического момента механизма, т.е
. (4-5)
Рабочие механизмы создают статические моменты 
.
Если для любого электродвигателя входной величиной является статический момент механизма, а выходной – его скорость, то есть скорость является функцией момента, то для механизмов, наоборот, входной величиной является скорость ω, а выходной статический момент механизма 
, момент является функцией скорости.
Это означает, что при любом изменении скорости механизма или скорости двигателя будет изменяться статический момент (момент сопротивления) механизма 
.
Рассмотрим типичные зависимости статического момента сопротивления от угловой скорости.
Различают два основных вида механических характеристик судовых исполнительных механизмов:
1. Крановые, когда при изменении скорости в широких пределах статический момент не изменяется (рис. 4.1а, характеристика 1).
Такая характеристика описывается уравнением
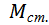(ω) 
= сonst (4- 6)
т.е. статический момент механизма 
не зависит от ω 
скорости дигателя.
2. Вентиляторные, у которых статический момент механизма пропорционален квадрату скорости (рис. 4.1а, характеристика 2).
Такая характеристика описывается уравнением
= 
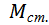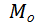+ Δ 
, (4- 7)
где 
– момент холостого хода;
Δ = сω 
– момент, создаваемый рабочим органом механизма при выполнении полезной работы (с – постоянный коэффициент, ω – угловая скорость вала механизма).
Рис. 4.1. Механические характеристики механизмов с крановыми характеристиками 1 и вентиляторными 2: а – в системе координат (ω); б – в системе координат ω (
)
Крановые характеристики имеют механизмы грузовых кранов, лебедок, брашпилей, т.е. механизмов, работа которых связана с преодолением действия силы тяжести. Статический момент крановых механизмов определяется следующим выражением
= GD/2 = const, (4-8)
где G – вес груза (у брашпилей – вес якоря с цепью);
D – диаметр грузового барабана(для брашпилей – якорного барабана, барабана швартовной лебёдки).
Вентиляторные характеристики имеют: центробежные насосы вентиляторы, гребные винты, компрессоры и другие механизмы, для которых сопротивление технологической среды (вода, масло, газы) зависит от квадрата скорости рабочего органа (крыльчатка, лопости и тд.).
У механизмов с вентиляторными характеристиками условия пуска – легкие, т.к. при пуске на валу механизма действует небольшой момент холостого хода 
, создаваемый только силами трения в элементах привода.
Однако при увеличении угловой скорости –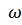 
трение лопастей о воздух, воду или другую среду увеличивается и по мере разгона статический момент механизма резко увеличивается за счет того, что к моменту холостого хода , добавляется тормозящий момент момент Δ = сω , пропорциональный квадрату скорости.
Для изображения механических характеристик двигателей в теории электропривода принято использовать систему координат
ω ( 
),
а для механических характеристик механизмов – «перевернутую» систему координат
(ω) .
Применение разных систем координат для двигателей и механизмов создает трудности при рассмотрении электромеханических свойств электропривода, состоящего из электродвигателя и механизма.
Поэтому на практике для изображения механических характеристик двигателей и механизмов принята единая система координат ω ( ), т.е система, принятая для механических характеристик электродвигателей.
В этой системе координат механические характеристики механизмов показаны на рис. 4.1б.
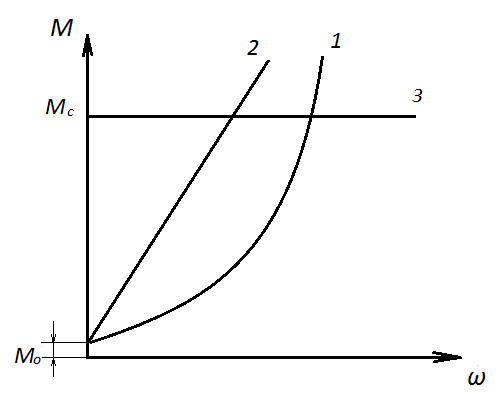
Рис.4.2Механические характеристики исполнительных механизмов:
1 – статический момент сопротивления механизма пропорционален квадрату угловой скорости; 2 – статический момент сопротивления механизма пропорционален угловой частоте вращения; 3 – статический момент сопротивления механизма не зависит от угловой частоты вращения вала механизма.
Статические моменты судовых механизмов
Статический момент (момент сопротивления) пропорционален частоте вращения (рис.4.2,кривая 2). В такой режим входит двигатель постоянного тока при динамическом торможении, когда якорь двигателя замкнут на резистор, а ток возбуждения не изменяется.
Статический момент (момент сопротивления) не зависит от частоты вращения (кривая 3). Характерно для подъемных кранов, лебедок, поршневых насосов при подъеме воды на постоянную высоту, транспортеров, конвееров с постоянной передвигаемой массой. Для пуска и ускорения таких механизмов двигатель должен развивать пусковой момент значительно больший их статического момента сопротивления.
Данные о статическом моменте (моменте сопротивления) механизма приводятся в технической инструкции. Для некоторых механизмов статический момент (момент сопротивления) зависит от траектории движения исполнительного механизма (от угла поворота). Например, в поршневом компрессоре, ножницах для резки металла, приводе рулевого устройства (Рис.4.3).
Рис 4.3 Механическая характеристика поршневого компрессора. Статический момент сопротивления зависит от траектории движения исполнительного механизма.
Иногда статический момент изменяется из-за изменения свойств обрабатываемого механизмами материала (вещества). И закономерности изменения момента сопротивление от скорости нельзя выразить ни графически, ни аналитически (например камнедробилки, бетономешалки).
Для электродвигателей угловая скорость и элетромагнитный момент связаны одинаковой зависимостью и обуславливают друг друга.
Статические моменты судовых механизмов могут быть функциями различных величин и поэтому признаку делятся на пять классов.
Моменты, не зависящие от параметров движения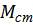 
= const (для грузоподъемных механизмов).
1. Моменты, зависящие от скорости: 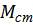= f(ω) для электромеханических преобразователей. Центробежных насосов, вентеляторов.
2. Моменты, зависящие от пути (угла поворота ) 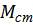= f(α ). Для шпилей, брашпилей.
3. Моменты, зависящие от скорости и угла поворота. 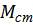= f( 
). Для электромеханических рулевых устройств.
4. Моменты, зависящие от времени 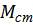= f (t). Для буксирных лебедок.
В общем случае статический момент механизма выражается уравнением,
+ (
) 
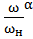(4-9)
где:
– начальный статический момент, создаваемый трением.
– номинальный момент нагрузки, соответствующий номинальной
скорости 
.
x – коэффициент нагрузки (выбирается в зависимости от характера нагрузки).
показатель степени, определяющий характер зависимости 
от
угловой скорости 
,(
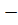1 < < 2) выбирается от 
1 до +2(для вентиляторов 2).
(4-10)
