Краткая теория. Этот метод широко применяется для определения коэффициента внутреннего трения сильно вязких жидкостей

Этот метод широко применяется для определения коэффициента внутреннего трения сильно вязких жидкостей, таких как глицерин и различные масла. Недостатком этого метода является то, что он требует значительного количества исследуемой жидкости. При движении шарика в вязкой жидкости возникает сила трения, величина которой зависит от коэффициента внутреннего трения жидкости.

В высокий цилиндрический сосуд с касторовым маслом бросают металлический шарик. На шарик, падающий в вязкой жидкости, действуют три силы:

1. Направленная вниз сила тяжести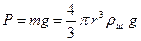

где r- радиус шарика, ρ_ш - плотность вещества, из которого сделан шарик, g - ускорение свободного падения.

2. Направленная вверх выталкивающая сила (архимедова сила), равная весу жидкости в объеме шарика

где r- радиус шарика, ρ_ж - плотность жидкости.

3. Сила трения F_тр. Эта сила направлена вверх, а ее численное значение находится по формуле Стокса

где r -радиус шарика, η- коэффициент внутреннего трения жидкости, υ- скорость движения шарика. Формула Стокса справедлива только для маленьких шариков, движущихся с небольшой скоростью. При увеличении размеров шариков и при возрастании скорости их движения возможно образование завихрений и сила трения становится пропорциональной более высокой степени скорости.

При движении шарика силы P и F _выт все время остаются постоянными, а сила трения возрастает по мере увеличения скорости. В начале движения сила F _тр очень мала и шарик движется ускоренно под действием силы, равной P –(F _выт.+ F _тр). С увеличением скорости увеличивается и сила F_тр и наступает такой момент, что направленные вверх силы F_тр и F_выт уравновесят направленную вниз силу тяжести Р.

или

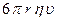= + (1)

После этого движение станет равномерным, и скорость можно найти, разделив путь 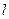, пройденный шариком, на время t его равномерного движения. Из формулы (1) находим, что

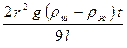= (2)

Эта формула справедлива для бесконечно широкого сосуда. Формула (2) является не совсем точной, так как при ее выводе не было уточнено то обстоятельство, что шарик, падая вниз, вытесняет жидкость. Вследствие этого создается поток жидкости вверх и возникает дополнительная сила. В случае относительно узкого сосуда и с учетом дополнительной силы в формулу (2) вводится поправка, учитывающая радиус сосуда.

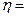
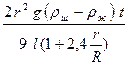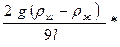
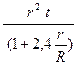= = А* (3)

где 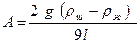, r- радиус шарика, R –радиус сосуда,

g = 9,8 м/с =980см/с.