Кроме выше перечисленных законов, используются также распределения Эрланга, Стьюдента, Лапласа и пр. Определение закона распределения отказов имеет большое значение при исследовании и оценке надежности. Определение  по одной и той же исходной информации, но при различных предположениях о законе распределения может привести к существенно отличающимся результатам. При выборе теоретического закона распределения необходимо учитывать информацию об изменениях, которые происходят в объектах перед наступлением отказов, т.е. о характере физических процессов, протекающих в объекте.
по одной и той же исходной информации, но при различных предположениях о законе распределения может привести к существенно отличающимся результатам. При выборе теоретического закона распределения необходимо учитывать информацию об изменениях, которые происходят в объектах перед наступлением отказов, т.е. о характере физических процессов, протекающих в объекте.
Закон распределения отказов можно определить по экспериментальным данным, но для этого необходимо проведение большого числа опытов в идентичных условиях. Практически эти условия, как правило, трудно обеспечить. Кроме того, такое решение содержит черты пассивной регистрации событий. Вместе с тем во многих случаях за время эксплуатации успевает отказать лишь незначительная доля первоначально имевшихся объектов. Полученным статистическим данным соответствует начальная (левая) часть экспериментального распределения. Более рационально – изучение условий, физических процессов при которых возникает то или другое распределение. При этом составляются модели возникновения отказов и соответствующие им законы распределения времени до появления отказа, что позволяет делать обоснованные предположения о законе распределения. Опытные данные должны служить средством проверки обоснованности прогноза, а не единственным источником данных о законе распределения. Такой подход необходим для оценки надежности новых изделий, для которых статистический материал весьма ограничен.
Экспоненциальный закон распределения характерен для внезапных отказов на интервале времени, когда период приработки объекта закончился, а период износа и старения еще не начался, т.е. для нормальных условий эксплуатации.
Нормальное распределение характерно для времени возникновения отказа, вызванного старением, этот закон используется для оценки надежности изделий при наличии постепенных (износовых) отказов.
Гамма-распределение широко применяется при описании появления отказов стареющих элементов, времени восстановления, наработки на отказ резервированных систем.
Распределение Вейбулла имеет место для отказов, возникающих по причине усталости тела детали или поверхностных слоев (подшипники, зубчатые передачи, развитие усталостной трещины в зоне местной концентрации напряжений, технологического дефекта или начального повреждения), а также отказов в процессе приработки.
Распределение Рэлея достаточно полно описывает поведение ряда объектов и элементов радиоэлектроники с явно выраженным эффектом старения и износа.
Для выбора закона распределения достаточно удобным является определение коэффициентов асимметрии и эксцесса с дальнейшим выдвижение и проверкой гипотезы о виде распределения.
Задача проверки гипотезы о законах распределения по коэффициентам асимметрии и эксцесса начинается с выбора нулевой гипотезы  . По данным эксперимента определяют статистические оценки коэффициента асимметрии
. По данным эксперимента определяют статистические оценки коэффициента асимметрии
 – величина, характеризующая асимметрию распределения случайной величины, и коэффициента эксцесса
– величина, характеризующая асимметрию распределения случайной величины, и коэффициента эксцесса  – мера остроты пика распределения случайной величины:
– мера остроты пика распределения случайной величины:
 ;
;
 ,
,
где  – среднеквадратическое отклонение;
– среднеквадратическое отклонение;
 – среднее значение;
– среднее значение;
 – третий центральный момент;
– третий центральный момент;
 – четвертый центральный момент.
– четвертый центральный момент.
Каждому закону распределений свойственно свое соотношение между коэффициентом асимметрии и коэффициентом эксцесса, которое может быть представлено диаграммой (рис. 1.14) с характерными областями и точками [8]. Например, точка  соответствует равномерному распределению, точка
соответствует равномерному распределению, точка  – нормальному, прямая 1 – логарифмически нормальному распределению, прямая 2 – закону Стьюдента, прямая 3 – гамма-распределению, области 1, 2, 3 соответствующему бета-распределению. Знание значений
– нормальному, прямая 1 – логарифмически нормальному распределению, прямая 2 – закону Стьюдента, прямая 3 – гамма-распределению, области 1, 2, 3 соответствующему бета-распределению. Знание значений  и
и  позволяет приближенно определить закон распределения, который следует выдвинуть в качестве гипотезы
позволяет приближенно определить закон распределения, который следует выдвинуть в качестве гипотезы  . При попадании точки в области диаграммы, для которых не определен закон распределения, выдвижение гипотетического закона должно осуществляться на основании дополнительных априорных соображений.
. При попадании точки в области диаграммы, для которых не определен закон распределения, выдвижение гипотетического закона должно осуществляться на основании дополнительных априорных соображений.

Рисунок 1.14 - Диаграмма соотношения коэффициентов асимметрии и эксцесса
Проверка гипотезы о законе распределения может быть произведена по критерию согласия Колмогорова-Смирнова
 ,
,
где  и
и  соответственно статистическая (эмпирическая) и гипотетическая (теоретическая) функции распределения случайной величины
соответственно статистическая (эмпирическая) и гипотетическая (теоретическая) функции распределения случайной величины 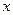 .
.
В качестве  пользуются функцией вида
пользуются функцией вида
 .
.
Если
 ,
,
где  табулированное значение при заданной доверительной вероятности
табулированное значение при заданной доверительной вероятности  (находится с помощью таблицы функции Колмогорова-Смирнова), то гипотеза
(находится с помощью таблицы функции Колмогорова-Смирнова), то гипотеза  о согласии эмпирического распределения и теоретического принимается.
о согласии эмпирического распределения и теоретического принимается.






