Пластинкой называют тело, имеющее форму прямой призмы, высота которого /г значительно меньше размеров основания а и Ь, рис. 1, 2, 3.

рис.2 рис.3
Плоскость, которая делит высоту пластинки пополам, называется срединной плоскостью. Теория изгиба пластин начинает свое развитие с работ Софи Жермен и Лагранжа.
Техническая теория тонких пластинок построена с использованием следующих гипотез [1,2]:
1. Гипотеза прямых, нормалей: любой прямолинейный элемент, нормальный к срединной плоскости, остается прямолинейным и нормальным к срединной поверхности после деформирования пластинки, и длина его не изменяется, то есть γxz = 0, γyz = 0, εz= 0.
2. Гипотеза о недеформируемости срединной плоскости: в срединной плоскости отсутствуют деформации растяжения, сжатия и сдвига, то есть она является нейтральной и ее перемещения U0= О, V0= 0 при z = 0.
3. Гипотеза об отсутствии давления между слоями пластинки, параллельными срединной плоскости: слои волокон, параллельные срединной плоскости, не давят друг на друга, то есть σz= 0.
Пластинки различают жесткие (сравнительно толстые), тонкие и мембраны (очень тонкие). Рассмотрим теорию расчета тонких упругих пластинок, для которых справедливы следующие соотношения: 1. Уравнение равновесия [1,2]:
 (1)
(1)
где Мx(х,у), Му(х,у), Н(х,у)- изгибающие и крутящий моменты.
2. Геометрические соотношения (соотношения Коши) [1,2]:


 (2)
(2)
где z - координата по толщине пластинки; w -прогиб пластинки, постоянный по ее толщине; εх, εу, γxy- деформации в произвольной точке пластинки; χx, χy -деформации в срединной плоскости пластинки; χ- деформация кручения срединной плоскости пластинки.
3. Физические соотношения (закон Гука) [1,2]:


 (3)
(3)
Интенсивности внутренних силовых факторов (изгибающих и крутящего моментов Мx (х,у), Мy(х,у), Н(х,у)) являются погонными величинами, отнесенными к единице длины сечения пластинки, измеряются в (НМ/М) и подсчитываются по формулам [1,2]:


 (4)
(4)
При подстановке в (4) выражений (3) формулы для погонных моментов Мх (x, у), My(х,у), Н(х,у) принимают вид [1, 2]:


 (5)
(5)
где D = Еh3 /[12(1-v2)] -цилиндрическая жесткость изгиба пластинки.
Подстановкой выражений (5) в (1) получаем уравнение равновесия элемента пластинки (уравнение Софи Жермен) [1, 2]:
 (6)
(6)
Уравнение (6) является неоднородным дифференциальным уравнением четвертого порядка в частных производных. В связи с этим для решения конкретной задачи по каждому направлению в пластинке необходимо задать четыре граничных условия: два на одном и два на другом крае. Рассмотрим варианты задания граничных условий.
Защемленный край. Если край пластины x= 0 защемлен, то прогиб в точках этого края равен нулю, и заделанное сечение пластины не поворачивается (плоскость, касательная к изогнутой срединной поверхности, совпадает со срединной плоскостью пластинки до изгиба) [1,2]:

 (7)
(7)
Условия типа (7) называются геометрическими.
Шарнирно-опертый край. Если край пластины х = 0 шарнирно оперт и может свободно поворачиваться, то прогиб и изгибающий момент на этом крае должны быть равны нулю [1,2]:

 (8)
(8)
В данном случае шарнирные опоры предполагаются жесткими (w= 0) и линия x= 0 остается неизогнутой. Поэтому обращаются в ноль производные:

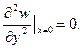
Тогда граничные условия для шарнирно опертого края будут:

 (9)
(9)
Условия типа (8) называются смешанными (статически геометрическими).
Свободный край. Если край x= 0 свободен от опорных закреплений, то для него обращаются в ноль изгибающие моменты Мх и приведенные поперечные силы Q*x (статические граничные условия) [1,2]:

 (10)
(10)
Переходим к изложению методики решения задач изгиба пластинок, основанной на использовании метода конечных разностей (МКР).
Суть метода конечных разностей состоит в замене разрешающего дифференциального уравнения для пластинок (6) и граничных условий, выраженных через функцию прогиба w и ее производные, конечно-разностными алгебраическими уравнениями. В результате задача сразу сводится к решению систем алгебраических уравнений с неизвестными значениями функции прогиба w в отдельных точках пластинки. Для двумерной области при использовании метода конечных разностей (МКР) вводится ортогональная сетка линий с шагами h1 по x и h2 по у (рис. 4).
Именно поэтому МКР называют иногда методом сеток. Очевидно, что при уменьшении величин шагов h1 и h2 возрастает число искомых величин функции прогиба в узлах сетки ik, jk (рис. 4) и, соответственно, точность получаемого по МКР решения. При этом, однако, повышается порядок решаемой системы линейных алгебраических уравнений (СЛАУ), поэтому необходим рациональный выбор шага сетки.

Рис.4
Главным в МКР является представление производных функции w(х,у) конечно-разностными соотношениями (аналогами). Для рассмотрения этого вопроса рассечем плоскость ХОУ (рис. 4) вертикальной плоскостью, параллельной плоскости ХОZ. и проходящей через центральную точку I, j сетки (рис. 4). Если теперь записать конечно-разностное соотношение для производной  простейшим образом, то получим формулы:
простейшим образом, то получим формулы:

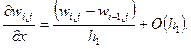 (11)
(11)
Первая из формул (11) является разностью «вперед», вторая - разностью «назад», а величина О(h1) указывает, что при использовании, например, формулы 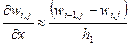 допускается существенная погрешность порядка величины шага сетки h1.
допускается существенная погрешность порядка величины шага сетки h1.
Очевидно, что для получения удовлетворительного по точности решения придется использовать весьма мелкую сетку, что неизбежно поведет к значительным трудностям при реализации алгоритма на ПЭВМ.
Именно поэтому более предпочтительна аппроксимация производной в виде «центральной» разности, когда [7]:
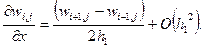 (12)
(12)
Величина погрешности аппроксимации  составляет теперь уже О(h12) - величину порядка квадрата шага сетки. Это позволяет решать задачи расчета пластинок на тех сетках, когда время счета на ПЭВМ является приемлемым, а точность решения - достаточно высокой, что и продемонстрировано далее.
составляет теперь уже О(h12) - величину порядка квадрата шага сетки. Это позволяет решать задачи расчета пластинок на тех сетках, когда время счета на ПЭВМ является приемлемым, а точность решения - достаточно высокой, что и продемонстрировано далее.
Используем в дальнейшем лишь «центральные» разности и приводим сводку формул для конечно-разностных аналогов производных от функции w(x,y) с погрешностью О(h12), О(h22), О(h1h2) [3, 7]:
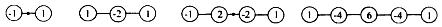





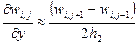 (11)
(11)



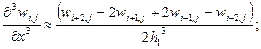






Графическое изображение первых четырех производных от w(x,y) по x приведено в первой строке (13).
С использованием формул (13) дифференциальный оператор уравнения Софи Жермен заменяется конечно-разностными соотношениями в узлах сетки xk, yi. Таким же образом заменяются и дифференциальные операторы, входящие в граничные условия для пластинок.
Заметим, что вид граничных условий определяет вид системы уравнений МКР, поэтому данный вопрос необходимо рассмотреть весьма подробно. На рис. 5 приведены известные варианты граничных условий для кромки x= а пластинки: шарнирное опирание (рис. 5 а), защемление, (рис. 5 б), свободный край (рис. 5 в).
а) б) в)

Рис. 5.
Точки на линии x=а относятся к контуру пластинки (контурные точки), точки на линии x=a+h1 - первый ряд (предконтурный) внутриконтурных точек. Точки на линии x=a+h1 - первый законтурный ряд точек. На рис. 5 показаны также вторые (внутриконтурный и законтурный) ряды точек.
Необходимость рассмотрения законтурных точек определяется непосредственно дифференциальным уравнением (6), записанным в центральных разностях (13). Действительно, если, например, записать дифференциальный оператор 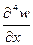 по (13) в точках с x=a-h1, рис. 5 а - шарнирныйкрай, рис. 5 б - заделанный край, то в формулу войдут значения прогиба в узлах x=a+h1 (законтурный узел), x= а (узел контура) и т.д. При записи данного оператора для точки с х = а (контур) (рис. 5 в), в формулу войдут уже значения прогиба в узлах x=a+2h1, x=a+h1 (законтурные узлы).
по (13) в точках с x=a-h1, рис. 5 а - шарнирныйкрай, рис. 5 б - заделанный край, то в формулу войдут значения прогиба в узлах x=a+h1 (законтурный узел), x= а (узел контура) и т.д. При записи данного оператора для точки с х = а (контур) (рис. 5 в), в формулу войдут уже значения прогиба в узлах x=a+2h1, x=a+h1 (законтурные узлы).
Заметим, что при шарнирном закреплении или жестком защемлении контура для точек на нем wi,j=0, поэтому конечно-разностные аналоги дифференциального уравнения (6) записываются лишь для точек внутри контура. Если же сторона контура свободна от закреплений, то на нем wi,j ≠0 и необходима запись конечно-разностного аналога уравнения Софии Жермен для точек данной стороны контура.
Рассмотрим также вопрос о законтурных значениях функций для всех условий на контуре.
Шарнирно-опертый край
Для точек на контуре имеем:
 (14)
(14)
(рис. 5 а), также в ноль на контуре обращаются изгибающие моменты:
 (15)
(15)
Конечно-разностный аналог (15) имеет вид:
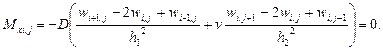 (16)
(16)
Так как точки (i; j); (i; j+1); (i; j-1) принадлежат контуру, то для них w=0, тогда получаем из (16) равенство:
 (17)
(17)
Окончательно имеем для шарнирно-опертого края равенство нулю прогибов на контуре и обратную симметрию (17) для прогибов точек за контуром и внутри него. Для вычисления поперечных сил в точках контура нужны величины прогибов в точках второго законтурного ряда - для шарнирно-опертого края будем иметь формулу 
Защемленный край
Для точек на контуре в этом случае также имеем равенство  (рис. 5 б). Равняются нулю и углы наклона касательной к поверхности пластинки по линии, перпендикулярной заделанному краю:
(рис. 5 б). Равняются нулю и углы наклона касательной к поверхности пластинки по линии, перпендикулярной заделанному краю:  И формул (13) при этом непосредственно получаем:
И формул (13) при этом непосредственно получаем:

 (18)
(18)
Таким образом, при защемлении края пластинки прогибы всех контурных точек равны нулю, а для прогибов точек за контуром и внутри него реализуется прямая симметрия. В частности, имеем равенство  для точек второго законтурного ряда.
для точек второго законтурного ряда.
Важно, что при этом использование формулы:
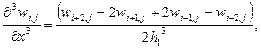
автоматически дает в контурном узле нулевое значение для поперечной силы в балке, вырезанной из пластинки.
Для устранения данного явного несоответствия с физическим смыслом задачи (на самом деле поперечная сила равна по модулю величине опорной реакции) рекомендуется использование формулы:
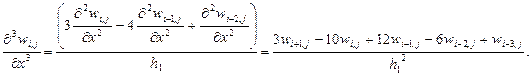 (19)
(19)
Заметим, что данное представление производной  устраняет все несоответствия, практически не снижая точности вычислений.
устраняет все несоответствия, практически не снижая точности вычислений.
Свободный край
При данных граничных условиях (рис. 5 в) на контуре обращаются в ноль: 1) изгибающий момент в плоскости, перпендикулярной краю пластинки; 2) приведенная поперечная сила. Записываем конечно-разностные аналоги данных условий для края х = а (рис. 5 в):
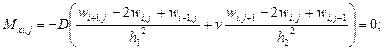 (20)
(20)

После элементарных преобразований из (20) получаются формулы для законтурных значений w:
 (21)
(21)

Таким образом, и при свободном крае законтурные значения функций выражаются через внутриконтурные значения (и значения на контуре).
Однако для расчета пластинок МКР необходим учет не только законтурных значений функции прогиба, но и ее значений за углами пластинки, о которых пока ничего не сказано. Рассмотрим все возможные варианты закрепления углов пластинки.
Угол без свободных от закреплений сторон
Возможны три варианта таких углов, а именно комбинации с шарнирным опиранием двух сторон, их защемлением и, наконец, комбинация «шарнирно-опертая сторона» - «защемленная сторона».

рис.6
Все три возможные комбинации изображены на рис. 6 а, б, в.
Во всех случаях конечно-разностные аналоги уравнения (6) записываются для узлов, помеченных на рис. 6 темными кружочками. При этом в уравнения входят как помеченные светлыми кружочками контурные значения функций (w = 0 в заделке или на шарнирно-опертом крае), так и законтурные величины, помеченные звездочками. Все они определяются по методике, изложенной выше.
Однако при решении задачи необходимы и величины в узлах, помеченных на рис. 6 квадратиками - они входят в формулы для изгибающих Мх, Му и крутящего Н моментов для угловых точек.
Считаем, что опоры как бы продолжаются до точек «в» и «г» (рис. 6) и получаем wВ =0, wГ=0.
С учетом свойств шарнирных опор для случая (рис. 6 а) имеем:
wБ=-w2=w1=-w3. (22)
С учетом свойств заделанных кромок для случая (рис. 6 6) имеем:
wБ=w2=w1=w3. (23)
С учетом свойств закрепленных сторон для случая (рис. 6 в) имеем:
wБ=-w2=-w1=-w3. (24)
Данные формулы позволяют вычислить изгибающие и крутящий моменты во всех узлах пластинки.
Угол с присутствием свободных от закреплений сторон
Возможны три варианта таких углов, приведенные на рис. 7.
Конечно-разностные аналоги дифференциального уравнения равновесия элемента пластинки (6) записываются для узлов, помеченных на рис. 7 темными кружочками. Законтурные значения, помеченные на рис. 7 звездочками, входят в данные уравнения и могут быть найдены из граничных условий на сторонах контура. Решаем вопрос о значениях функций в узлах, помеченных квадратиками (число данных узлов равно пяти).

рис.7
Для случая с двумя свободными сторонами (рис. 7 а) можно записать пять граничных условий:
1)МxD=0; 2) МуD=0; 3) HD=0; 4) Q*xD=0; 5) Q*yD=0. При совместном рассмотрении условий 1 и 2 получаем следующие уравнения:
wГ-2wД+wЕ=0, wF-2wД+wB=0. (25)
Условие 3 соответствует отсутствию сосредоточенной реакции в угловой точке  и дает уравнение
и дает уравнение
w1-w2+wБ-w3=0. (26)
Условия 4 и 5 нужны для вычисления значений w4 и w5, входящих в конечно-разностный аналог уравнения (6) для точки «Д» и в формулы для QxD, QyD, Q*xD, Q*yD. Использование данных условий дает уравнения:
 (27)
(27)

позволяющие выразить w4 и w5 через значения прогиба в других точках.
Для случая, показанного на рис.7 б (свободная сторона — защемленная сторона), можно записать пять граничных условий: 1) 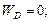 2)
2) 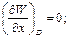 3)
3)  4)
4)  5)
5) 
На основании свойств прямой симметрии для защемленной стороны;ластинки (18) можно записать равенства:
wГ=wE, w4=wK, wБ=w2. (28)
Условие 3 дает равенство:
wВ=wF=0 (29)
Условие 5 дает уравнение:
 (30)
(30)
позволяющее выразить w5 через значения прогиба в других точках.
Отметим, что при такой записи условий в узле подсчитываются величины wГ=wE≠0, что приводит к нарушению условия 4 при записи его в центральных конечных разностях. Однако при этом результаты расчетов МКР согласуются с данными по другим методам расчета пластинок и полностью соответствуют физическому смыслу задачи.
Если же принять [3] wГ=wE=0 для удовлетворения условия 4 (при записи его в центральных конечных разностях), то прогиб в узле на свободной от закреплений стороне контура wE=0, что явно противоречит физическому смыслу решаемой задачи, и результаты расчетов МКР качественно отличаются от известных данных других авторов [4].
Для случая, показанного на рис. 7 в (угол, образованный шарнирно-опертой стороной и свободной стороной) можно записать пять граничных условий:
1) 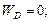 2)
2) 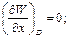 3)
3)  4)
4) 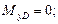 5)
5) 
На основании свойств обратной симметрии при шарнирном опирании 1 7) можно записать равенства:
wГ=-wE, w4=-wK, wБ=-w2. (31)
Условие 2 дает равенство:
wВ=wF=0 (29)
Условие 5 дает уравнение, совпадающее с уравнением (30), из которого с учетом (31) и (32) следует:
w5=0. (33)
Таким образом, все возможные варианты закрепления сторон и углов пластин рассмотрены, что позволяет рассмотреть примеры расчетов МКР.






