Преобразуем треугольник, образуемый элементами 1, 3, 5, в звезду с элементами 6, 7, 8 (рис. 2.22.). Согласно формулам (2.74) рассчитываем вероятности отказов элементов звезды:
.
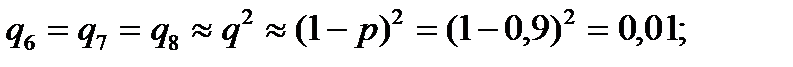
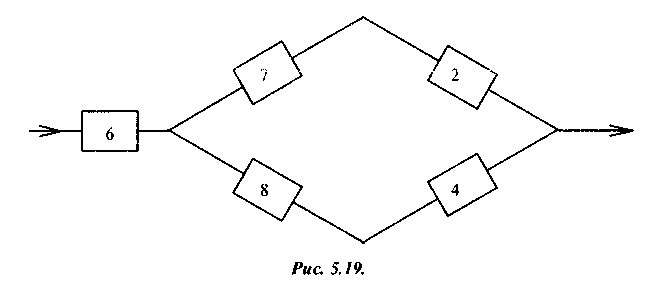
Рис. 2.22.
Используя формулы для последовательно и параллельно соединенных элементов, определяем вероятность безотказной работы системы:
.
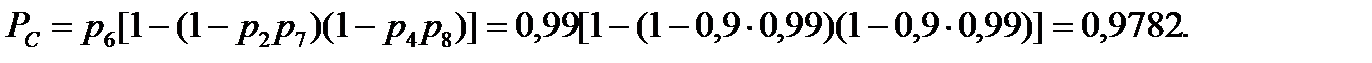Решим этот же пример методом исключения элементов. В качестве исключаемого выберем элемент 5. Рассмотрим две структуры. В первой из них в месте расположения элемента 5 будет короткое замыкание (рис. 2.23.). Поэтому получим
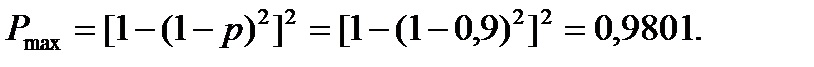
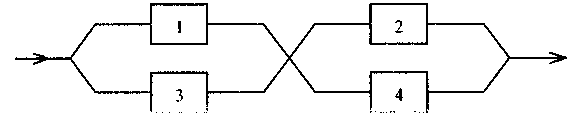
Рис. 2.23.
Во второй структуре в месте нахождения элемента 5 будет разрыв цепи (рис. 2.24.).
Поэтому имеем
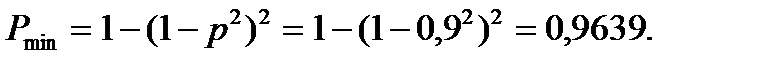
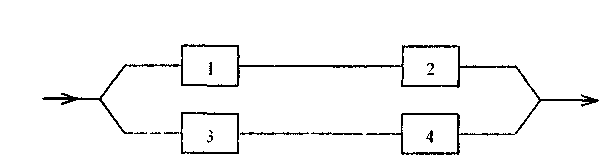
Рис. 2.24.
С учетом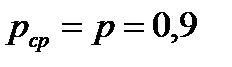 
на основании (2.80) окончательно получаем
= 0,9639+(0,9801-0,9639) 0,9 = 0,9785.
Сравнение значений вероятностей безотказной работы, полученных рассмотренными приближенными методами, показывает, что они очень близки.
