Для сгруппированных данных статистические числовые характеристики выражаются приведенными ниже формулами.
Статистическое среднее математическое ожидание определяется как
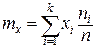, (3)
где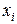 
― середины интервалов 
, k ― число интервалов группирования случайной величины.
Статистическая средняя дисперсия является характеристикой рассеивания случайной величины – разбросанности ее значений около математического ожидания, и определяется по формуле:
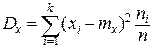. (4)
После перегруппирования интервалов в таблице 2, число интервалов k = 5 (см. табл. 3), а значения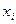 
= / 2 приведены в таблице 4.
Статистическое среднее математическое ожидание, рассчитанное по формуле (3), составляет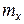 
=0,1376.
Дисперсия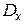 
=0,0196.
Таблица 4
| Интервалы,
| 
|
| |
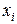
| 0,0000 | 0,046 | 0,0230 | |
| 0,046 | 0,0945 | 0,0702 | |
| 0,0945 | 0,1891 | 0,1418 | |
| 0,1891 | 0,2836 | 0,2364 | |
| 0,2836 | 0,6618 | 0,4727 |
Статистические среднее квадратическое отклонение и коэффициент вариации случайной величины составляют:
,
.
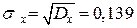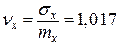Величина коэффициента вариации весьма близка к единице, что характерно для экспоненциального закона распределения.
Центральные моменты рассчитываются по формуле
.
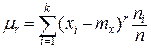Центральные моменты 3-го и 4-го порядков:
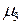= -0,0044, 
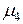= 0,0016.
Рассчитаем также другие часто применяемые числовые характеристики случайных величин ― асимметрию и эксцесс.
Асимметрия Sk:
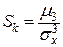, Sk = 1,595.
Для симметричных распределений Sk = 0.
Четвертый центральный момент служит для характеристики крутости распределения и описывается с помощью эксцесса:
,
.
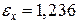5. Гистограммы и определение закона распределения
случайной величины
Для наглядного представления об эмпирическом распределении строится гистограмма (ступенчатая диаграмма) эмпирической плотности распределения случайной величины (рис. 7). По оси абсцисс откладываются интервалы (разряды) случайной величины x, и на каждом из интервалов строится прямоугольник с площадью, равной частоте появления случайной величины в данном интервале. Высоты прямоугольников пропорциональны соответствующим частотам и равны эмпирической плотности вероятности / n для каждого интервала.
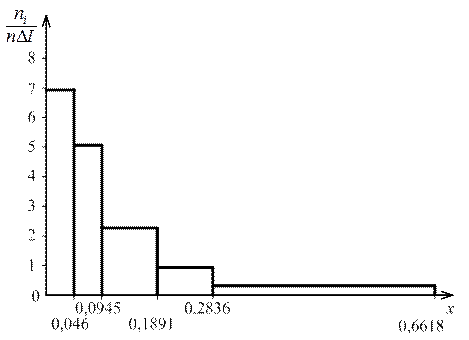
Рис. 7. Ступенчатая диаграмма эмпирической плотности вероятности
В данном случае вид теоретической функции распределения случайной величины заранее не известен. Основой для подбора той или иной теоретической дифференциальной функции (плотности) распределения, служит внешний вид гистограммы. Сопоставив гистограмму, построенную по данным таблицы 3 (рис. 7), с теоретическими кривыми распределения, можно предположить, что анализируемая случайная величина подчиняется экспоненциальному закону распределения.
Экспоненциальный закон характеризуется плотностью распределения вида
,
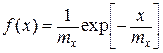где 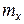― статистическое среднее математическое ожидание.
Рассчитанные значения плотности распределения на границах интервалов сведены в таблице 5.
Таблица 5
| Границы интервалов |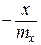 
| 
|
|
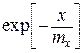
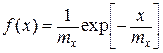
| 7,2674 | |||
| 0,0460 | -0,3343 | 0,7157 | 5,2013 |
| 0,0945 | -0,6871 | 0,5030 | 3,6557 |
| 0,1891 | -1,3742 | 0,2530 | 1,8389 |
| 0,2836 | -2,0613 | 0,1273 | 0,9250 |
| 0,6618 | -4,8098 | 0,0081 | 0,0592 |
На гистограмме (рис. 8) по данным таблицы 5 построена выравнивающая кривая распределения, представляющая собой график теоретической функции f(t),которая, сохраняя в основном существенные особенности статистического распределения, свободна от случайных неправильностей хода гистограммы.
6. Определение степени соответствия теоретического
распределения данным эксперимента
При подборе теоретической кривой распределения между нею и статистическим распределением неизбежны некоторые расхождения. При этом необходимо знать, объясняются эти расхождения только случайными обстоятельствами, связанными с ограниченным числом опытных данных, или они являются существенными и связаны с тем, что подобранная кривая плохо выравнивает данное статистическое распределение.
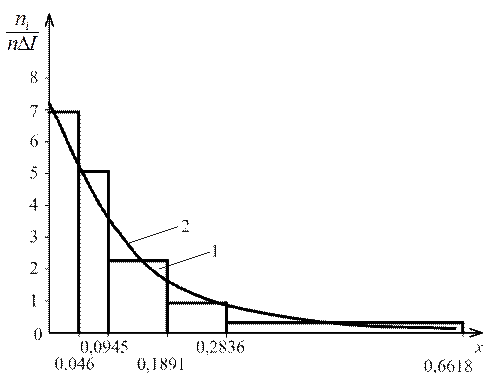
Рис. 8. Гистограмма (1) и выравнивающая кривая (2) экспоненциального распределения
Степень соответствия между выдвинутой гипотезой со статистическим материалом устанавливается с помощью критериев согласия.
Наиболее распространенным является критерий К. Пирсона 
, величина которого рассчитывается по формуле
, (4)
где k ― число интервалов группирования случайной величины; ni ― число значений случайной величины в i -м интервале; n ― общее число полученных значений случайной величины; p ― теоретическая вероятность попадания случайной величины в i- й интервал.
Теоретическая вероятность попадания случайной величины X в i -й интервал равна приращению функции распределения на этом интервале:
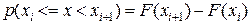. (5)
Функция экспоненциального распределения описывается формулой
,
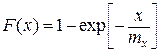поэтому формулу (5) можно представить как
.
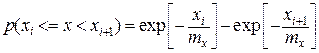Значения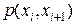 
приведены в таблице 6.
Таблица 6
| Границы интервалов |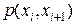
|
| - | |
| 0,046 | 0,2843 |
| 0,0945 | 0,2127 |
| 0,1891 | 0,2500 |
| 0,2836 | 0,1258 |
| 0,6618 | 0,1191 |
По формуле (4) и данным таблиц 3 и 6 находим значение критерия согласия Пирсона =1,53.
Число степеней свободы распределения определяется по формуле
r=k-s,
где k ― число интервалов группирования случайной величины; s ― число независимых условий (связей), налагаемых на частоты.
Для экспоненциального закона распределения s = 2, следовательно, число степеней свободы в рассматриваемом случае составляет r = 5 – 2 = 3.
Пользуясь таблицей значений вероятностей для критерия , находим вероятность того, что эмпирическое распределение подчиняется экспоненциальному закону. Если получаемая вероятность составляет более 10 %, то обычно считается, что экспериментальные данные не противоречат принятому теоретическому закону распределения случайной величины.
Для =1,53 и r =3 значение вероятности находится в пределах между 50 и 70 %, значит, предположение о том, что экспериментальные данные подчиняются экспоненциальному закону распределения, является верным.
Заключение о надежности объекта
В результате обработки исходной статистической информации о надежности объекта, представленной в виде статистического ряда (см. табл. 1), установлены:
― средняя наработка на отказ объекта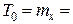 
0,138;
― вид закона распределения случайной величины x
;
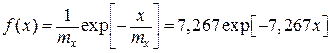― аналитическое выражение для определения вероятности безотказной работы объекта
.
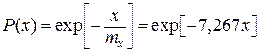Итак, установлено, что исходные экспериментальные данные подчиняются экспоненциальному закону распределения. Экспоненциальному закону распределения подчиняются случайные значения времени работы между отказами или до отказа объектов, для которых характерны внезапные отказы.
