Силы, действующие при захвате металла валками

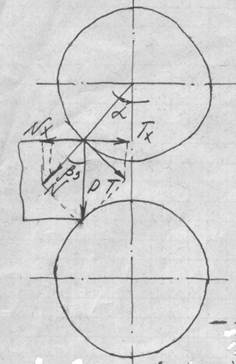
При соприкосновении полосы с валками каждый (в точке касания с полосами) из них оказывает на полосу действие в виде силы N, направленной нормально к поверхности валка и силы трения T, направленной по касательной.

Сила трения определяется по формуле:

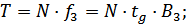
f ₃– коэффициент трения при захвате.

β₃ – угол трения при захвате, т.е. угол, тангенс которого равен f ₃.

Рассмотрим при каких условиях валки смогут захватить полосу и обеспечить ее движение (прокатку).

Рисунок 1. Схема действия сил в

начинающем моменте захвата

Проектируя силы N и T, действующие на полосу в момент соприкосновения её с валками на горизонтальную ось, получим силы Nx и Tx, действующие на полосу в противоположных направлениях.

Сила Tx – втягивает полосу в валки, а сила Nx – восстанавливает ее Рисунок 1.

Захват полосы валками произойдет при условии: Tx ≥ Nx.

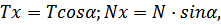следовательно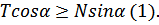

Подставим в уравнение (1) значение T, получим: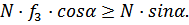

Сократив обе части неравенства на N и разделив на cosα получим условие захвата полосы валками:

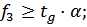
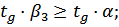
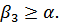
Следовательно захват полосы валками произойдет только тогда, когда тангенс угла захвата будет меньше коэффициента трения, или когда угол захвата будет меньше угла трения.

Об условиях захвата можно судить по положению равнодействующей силы P. Отклонение этой силы от положения вертикали в сторону прокатки свидетельствует о том, что горизонтальная проекция втягивающей силы Tx больше горизонтальной проекции выталкивающей силы Nx и захват возможен.

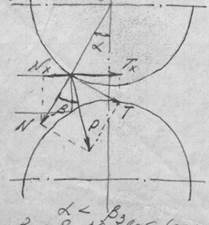В это случаем Рисунок 2.

При соотношении углов 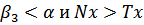равнодействующая направлена от вертикали в сторону противоположную направлению прокатки, что свидетельствует о невозможности захвата полосы валками в данных условиях Рисунок 3.

Рисунок 2. Захват возможен.