Центральную тенденцию выборки позволяют оценить такие статистические характеристики, как среднее арифметическое значение, мода, медиана.
Наиболее просто получаемой мерой центральной тенденции является мода. Мода – это такое значение в множестве наблюдений, которое встречается наиболее часто. В совокупности значений (2, 6, 6, 8, 7, 33, 9, 9, 9, 10) модой является 9, потому что оно встречается чаще любого другого значения. В случае, когда все значения в группе встречаются одинаково часто, считают, что эта группа не имеет моды.
Когда два соседних значения имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений.
Если два несмежных значения в группе имеют равные частоты, и они больше частот любого значения, то существуют две моды (10, 11, 11, 11, 12, 13, 14, 14, 14, 17); в таком случае группа измерений или оценок является бимодальной.
Наибольшей модой в группе называется единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть несколько меньших мод. Эти меньшие моды представляют собой локальные вершины распределения частот.
Медиана (Me) – середина ранжированного ряда результатов измерений. Если данные содержат четное число различных значений, то медиана есть точка, лежащая посередине между двумя центральными значениями, когда они упорядочены.
Среднее арифметическое значение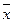 
для неупорядоченного ряда измерений вычисляют по формуле:
, (2.2)
где 
. Например, для данных 4,1; 4,4; 4,5; 4,7; 4,8 вычислим :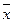
.
Каждая из выше вычисленных мер центра является наиболее пригодной для использования в определенных условиях.
Мода вычисляется наиболее просто – ее можно определить на глаз. Более того, для очень больших групп данных это достаточно стабильная мера центра распределения.
Медиана занимает промежуточное положение между модой и средним с точки зрения ее вычисления. Эта мера получается особенно легко в случае ранжированных данных.
Среднее множество данных предполагает в основном арифметические операции.
На величину среднего влияют значения всех результатов. Медиана и мода не требуют для определения всех значений. Посмотрим, что произойдет со средним, медианой и модой, когда удвоится максимальное значение в следующем множестве:
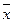Me Мода
Множество 1: 1, 3, 3, 5, 6, 7, 8 33/7 5 3
Множество 2: 1, 3, 3, 5, 6, 7, 16 41/7 5 3
На величину среднего особенно влияют результаты, которые называют “выбросами”, т.е. данные, находящиеся далеко от центра группы оценок.
