В процессе наблюдения или измерения какого-либо показателя получают ряд чисел. Численные результаты подразделяют на дискретные и непрерывные. К дискретным относят число подтягиваний на перекладине, число попыток и т.д., то есть результаты, выражаемые целым числом; к непрерывным – время прохождения дистанции, время реакции, скорость движения и т.п., то есть результаты, которые могут выражаться дробным числом, в частности, бесконечной дробью.
Генеральной совокупностью называется совокупность всех объектов, характеристики которых требуется определить. Выборочной совокупностью, или просто выборкой, называется часть объектов, случайным образом выделенных из общей генеральной совокупности. Например, длина тела студентов какого-либо вуза Республики Беларусь – выборочная совокупность, а длина тела студентов всех вузов – генеральная; в то же время длина тела студентов Беларуси – выборка по отношению к генеральной совокупности – всем студентам земного шара.
Генеральную совокупность мысленно можно представить так: это все объекты наблюдения (например, спортсмены), которые обладают теми же свойствами, что и объекты выборки.
Один из центральных вопросов статистики: как обобщить результаты, полученные на выборке, на всей генеральной совокупности?
Предположим, что исследователь проводил эксперименты на группе тяжелоатлетов III разряда и нашел, что один из методов тренировки лучше, чем другие. Можно ли распространить его данные на всех тяжелоатлетов III разряда, или же сделанные им выводы справедливы только для той группы спортсменов, в которой проводился эксперимент? Если исследованием охвачена вся генеральная совокупность, оно называется сплошным. Например, если кому-либо удалось обследовать всех сильнейших спортсменов мира в каком-либо виде спорта, значит. проведено сплошное исследование. Все остальные исследования называются выборочными. Одной из основных характеристик выборки является ее объем – n, который определяется числом объектов наблюдения, например, спортсменов в данном исследовании. Как проводится упорядочение и анализ выборки? Предположим, что у баскетболистов БГУФК измерили силу левой кисти. Результат измерений в килограммах (n = 100) представлен в таблице 2.1.
Таблица 2.1
Пример выборочных результатов (n = 100).
| № п/п | ... | ||||||||
| x, кг | ... | ||||||||
| x, кг (ранжиров.) | ... |
В этой таблице числа записаны в той последовательности, в какой проходили измерения, т.е. случайным образом. Такие данные представляют неупорядоченную выборку. Третья строка – выборка упорядоченная, точнее – ранжированная. Ранжированием называют расстановку результатов измерений в порядке возрастания или убывания.
Выборки большого объема разбивают на интервалы. В простейшем случае их может быть два. Например, когда необходимо отобрать худших или лучших спортсменов. Однако, для получения достаточно точных результатов число интервалов (его обозначают буквой k) должно быть больше (табл. 2.2).
Таблица 2.2
Рекомендуемое число интервалов для выборки разного объема.
| Объем выборки (n) | 10 – 20 | 30 – 50 | 60 – 90 | 100 – 200 | 300 – 400 |
| Число интервалов (k) | 5 – 6 |
Тогда величина, или шаг интервала, определяется:
(2.1)
где 
– максимальный результат измерений в выборке,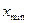 
– минимальный результат.
На основе значений k и h заполняют таблицу 2.3.
Таблица 2.3
Вариационный ряд измерений.
| № интервала | Граница интервала | Частота |
| 35,5 – 40,5 | ||
| 40,5 – 45,5 | ||
| 45,5 – 50,5 | ||
| 50,5 – 55,5 | ||
| 55,5 – 60,5 | ||
| 60,5 – 65,5 | ||
| 65,5 – 70,5 | ||
| 70,5 – 75,5 |
В столбец 1 записываем порядковые номера интервалов.
Столбец 2 получают следующим образом: выбирают значение x (нижнюю границу 1-го интервала) чуть меньше, чем 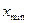(из табл. 2.1) – 35,5+5 = 40,5; получают верхнюю границу 1-го интервала (она же является нижней границей 2-го интервала); далее 40,5+5= 45,5 и т.д.
Столбец 3 определяет частоту, или «встречаемость», значений выборки в каждом интервале. Она определяется числом результатов измерений, попавших в данный интервал. Сумма частот всех интервалов всегда равна объему выборок.
Из этой таблицы можно определить, как часто каждое значение результатов измерений встречается в каждой выборке. Распределение, представленное в столбцах 2 и 3, в статистике называют вариационным рядом.
Анализ вариационных рядов упрощается при графическом представлении. Рассмотрим основные графики вариационного ряда.
1. Полигон распределения (рис. 2.1). График строится в прямоугольной системе координат. Величины измеряемого показателя откладываются на оси абсцисс, частоты (частости) – на оси ординат.
Рис. 2.1. Полигон распределения (на оси абсцисс – середины интервалов,
по оси ординат– частоты).
2. Гистограмма распределения (рис. 2.2). График строится аналогично полигону распределения, однако на оси абсцисс откладываются не точки (середины интервалов), а отрезки, отображающие интервал, и вместо ординат, соответствующих частотам или частостям отдельных вариантов, строят прямоугольники с высотой, пропорциональной частотам и интервалам.
35,5 40,5 45,5 50,5 55,5 60,5 65,5 70,5 75,5
Рис. 2.2. Гистограмма (по оси абсцисс – интервалы, по оси ординат – частоты).
