Математические основы теории надежности

Теория надежности развивается по нескольким направлениям и одно из основных – математические основы теории надежности [3-11]. Эти основы ищутся в теории вероятностей и в ее части – математической статистике.

Важнейшими характеристиками здесь считаются: безотказность, ремонтопригодность, долговечность и сохраняемость. Первые две признаются основными для химической индустрии.

Безотказность количественно описывается 8-ю показателями:

1. P(t) – вероятность безотказной работы, ,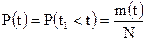
где m(t) – число исправных элементов, N – общее число наблюдаемых элементов.

2. l(t) – интенсивность отказов, .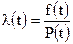

3. Т₁ – средняя наработка до отказа, это математическое ожидание наработки элемента до 1 – го отказа.

4. Т – средняя наработка между отказами.

5. W(t) – ведущая функция потока отказов.

6. w(t) - параметр потока отказов, т.е. средняя частота потока отказов.

7. Q(t) – вероятность отказа в интервале времени (0,t).

8. f(t) - частота или плотность распределения отказов.

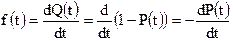
Статистический характер этих показателей определяет и метод их нахождения:

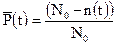, где N₀ - число изделий в начальный момент времени, n(t) – число отказавших изделий за время t;

;

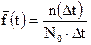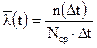, где N_cp – число изделий, исправно работающих в интервале времени Dt;

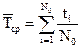, где t_i – время безотказной работы i-го изделия.

Здесь в этих формулах черта сверху означает символ оценки величины

.

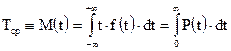Исходя из математического смысла этих показателей, зная один из них, не сложно найти все другие.

Чтобы этот математический аппарат начал работать, чтобы получить количественно эти критерии надежности, приходится использовать различные распределения вероятностей случайных событий: экспоненциальное, усеченное гауссовское, Релея, g-распределение, Вейбула, логарифмически нормальное и т.д. Наиболее распространенное распределение в теории надежности - экспоненциальное. Оно хорошо описывает (аппроксимирует) внезапные отказы элементов в установившемся режиме работы, а также для описания сложных систем, элементы которых восстанавливаются в процессе работы системы.

Основное свойство экспоненциального распределения - отсутствие “памяти” элемента о прошлом, зато экспериментально искать надо только один параметр в распределении. Нормальное распределение хорошо подходит для описания постепенных отказов, возникающих в результате деградации, износа. Но здесь приходится искать два параметра распределения.

Испытания на надежность [6, 7, 11] проводят с целью нахождения параметров функции распределения. Здесь проводят испытания изделий и далее применяют методы статистики. Используют Б-планы (отказавшие элементы не заменяются новыми), В-планы (с заменой), Т-планы (наблюдение ведется в течении Т времени), r-планы (наблюдения ведутся до появления r-го отказа).

Для увеличения надежности систем используют различные приемы. В частности, в [3, 9, 10] подробно исследуются различные виды резервирования и показываются способы расчета показателей надежности систем с разными видами резервирования.