Т 11 t 11 Т 12 t 12 Т 13
 |
Т 11 t 11 Т 12 t 12 Т 13
Т 11 t 11 Т 12 t 12 Т 13
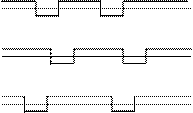
Рис.4
Процесс функционирования элементов СЭС показан на рис.4. Элемент Т 1, проработав случайное время Т 11, отказывает, а затем восстанавливается за время t 11. После восстановления он функционирует снова и проработав время Т 12, отказывает, восстанавливается за время t 12 и т.д. Совокупность отказов элементов СЭС во времени образует поток отказов.
Поток отказов называется стационарным, если вероятность появления событий на интервале t к, t к + D t к зависит от длины интервала и не зависит от момента t к начала интервала.
Поток отказов называется ординарным, если вероятность совмещения двух и более событий в один и тот же момент времени исчезающе мала, т.е.
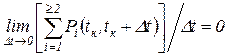, (26)
где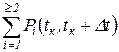 
- вероятность отказов двух и более элементов за время от tк до tк + D t.
Ординарность потока отказов означает, что в момент времени tк не может быть более одного отказа.
Поток событий называется потоком без последствий, если для любых непересекающихся событий, попадающих в один из них, не зависит от числа событий, попадающих в другие интервалы. Отсутствие последствий означает, что вероятность наступления n отказов за отрезок D t не зависит от того, сколько было отказов ранее и как они распределены во времени, то есть все отказы являются независимыми событиями.
В реальных СЭС ни одно из указанных свойств в точности не соблюдается. При отказе одного из элементов может произойти перераспределение нагрузки на оставшиеся элементы таким образом, что и эти элементы откажут, то есть нарушится отсутствие последствия. Нарушается и свойство ординарности. Однако исследования показали, что в инженерных расчетах надежности СЭС можно принять, что поток отказов удовлетворяет условиям стационарности, ординарности и отсутствия последствия. Такой поток отказов называется простейшим. При простейшем потоке отказов частота отказов
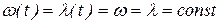, (27)
то есть интервалы между отказами в период нормальной работы оборудования распределены по экспоненциальному закону.
В качестве параметра экспоненциального распределения восстановления используют интенсивность восстановления m. Вероятность восстановления элемента за время от 0 до t:
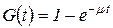; (28)
среднее время восстановления:
.
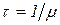Для инженерных расчетов надежности в СЭС принимается, что время безотказной работы T и время восстановления t распределяется по экспоненциальному закону.
