Критерием согласия называется критерий проверки гипотезы о том, что статистическое распределение согласуется с каким-либо известным законом (нормальным, экспоненциальным, Вейбулла и т. д.)
Имеется несколько критериев согласия: Колмогорова, Пирсона и т. д.
Критерий Пирсона не требует построения самого закона распределения. Достаточно задаться только общим видом функции F(t), а входящие в нее числовые параметры определяются по данным эксперимента.
Предположим, что произведено n независимых опытов, в каждом из которых случайная величина принимает определенное значение. Результаты опытов оформлены в виде статистического ряда с числом разрядов К.
| 
| 
| … | 
|
| 
| 
| … | 
|
| 
| 
| … | 
|
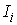
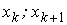
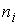
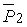
n – общее число значений случайной величины;
ni – число значений в i -ом разряде;
– статистическая вероятность i -ом разряде.
Требуется проверить, согласуются ли экспериментальные данные с гипотезой, что случайная величина Х имеет данный закон распределения. Этот закон распределения называется теоретическим. Из теоретического закона определяются теоретические вероятности попадания случайной величины в каждый разряд:
Сущность критерия согласия Пирсона состоит в сравнении теоретических и статистических вероятностей.
В качестве критерия проверки гипотезы принимают случайную величину
(3.72)
Эта величина при 
стремится к закону распределения 
с r степенями свободы. Число степеней свободы находят по равенству
, (3.73)
где k – число интервалов;
s – число параметров предполагаемого распределения, которые вычислены по экспериментальным данным.
Если предполагаемое распределение нормальное, то оценивают два параметра: математическое ожидание и среднеквадратичное отклонение. Поэтому
s = 2 и число степеней свободы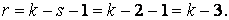 
Если статистические данные распределены по экспоненциальному закону, то оценивают параметр l, поэтому s = 1 и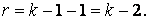 
Пользуясь таблицами распределения 
можно для вычисленной по формуле (3.72) меры расхождения и числа степеней свободы r найти вероятность P того, что величина, распределенная по закону превзойдет эту меру. Если эта вероятность мала, меньше или равна 0,1, событие с такой вероятностью можно считать практически невозможным.
Гипотезу о том, что закон распределения X есть F(x) следует считать неправдоподобной. Если же вероятность Р больше 0,1, гипотезу о том, что величина X распределена по закону F(x) следует считать правдоподобной, не противоречащей опытным данным.
Последовательность операций при использовании критерия Пирсона.
1. Определяется мера расхождения опытного и теоретического закона
где ni – количество значений случайной величины в i -ом интервале;
n – общее число значений случайной величины;
– частота повторения событий или статистическая вероятность в i -ом интервале.
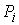– теоретическая вероятность события в i -ом интервале (из теоретической кривой);
k – число разрядов (интервалов);
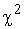– наблюдаемое значение критерия.
2. Определяется число степеней свободы распределения 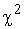по формуле
.
3. Пользуясь таблицами распределения 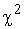, возможно для значения 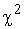, вычисленного в пункте 1 и числа степеней свободы r определить вероятность Р. Если эта вероятность мала (Р £ 0,1), гипотеза о совпадении опытного и теоретического законов отбрасывается. Если Р > 0,1, гипотезу можно принять не противоречащей опытным данным.
