ƒл€ определени€ доверительного интервала случайной величины, распределенной по симметричному закону, близкому к нормальному, используетс€ распределение —тьюдента. ѕри несимметричном законе примен€ют распределение ѕирсона или распределение c2.
ƒифференциальна€ функци€ распределени€ c2 имеет вид:

–аспределение c2 зависит от одного параметра r, называемого числом степеней свободы.
—оставлены специальные таблицы распределени€ c2, пользу€сь которыми, можно по заданной доверительной веро€тности  и числу степеней свободы r найти значение квантил€ распределени€ c2.
и числу степеней свободы r найти значение квантил€ распределени€ c2.
 ѕри экспоненциальном законе распределени€ отказов оценки параметров
ѕри экспоненциальном законе распределени€ отказов оценки параметров

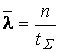 ,
,  , (3.64)
, (3.64)
где n Ц число отказов в интервале времени 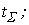
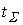 Ц суммарна€ наработка.
Ц суммарна€ наработка.
ƒл€ неремонтируемых элементов (объектов)
 (3.65)
(3.65)
где 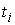 Ц врем€ исправной работы i -го отказавшего элемента (объекта);
Ц врем€ исправной работы i -го отказавшего элемента (объекта);
N Ц количество объектов;
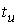 Ц врем€ испытаний;
Ц врем€ испытаний;
n Ц число отказавших объектов.
¬ случае, когда испытани€ провод€тс€ до тех пор, пока не откажут все выставленные на испытани€ объекты, суммарна€ наработка
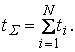 (3.66)
(3.66)
ƒл€ ремонтируемых объектов
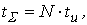 (3.67)
(3.67)
где 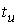 Ц длительность испытаний.
Ц длительность испытаний.
ƒоверительный интервал дл€ интенсивности отказов, в этом случае, находитс€ с помощью таблицы c 2, в которой параметрами €вл€ютс€ доверительна€ веро€тность  и число степеней свободы r.
и число степеней свободы r.
Ќижн€€ 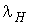 и верхн€€
и верхн€€ 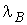 границы интенсивностей отказов:
границы интенсивностей отказов:
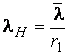 , где
, где  (3.68)
(3.68)
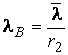 , где
, где  (3.69)
(3.69)
¬ формулах: 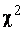 Ц квантили распределени€
Ц квантили распределени€  при числе степеней свободы
при числе степеней свободы 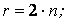
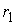 ,
, 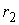 Ц коэффициенты.
Ц коэффициенты.






