Построение кодов Хемминга базируется на принципе проверки на чётность веса W (числа единичных символов) в информационной группе кодового блока.
Поясним идею проверки на чётность на примере простейшего корректирующего кода, который так и называется, кодом с проверкой на чётность или кодом с проверкой по паритету (равенству).
В таком коде к кодовым комбинациям безызбыточного первичного двоичного k -разрядного кода добавляется один дополнительный разряд (символ проверки на чётность, называемый проверочным, или контрольным). Если число символов «1» в исходной кодовой комбинации чётное, то в дополнительном разряде формируют контрольный символ «0», а если число символов «1» нечётное, то в дополнительном разряде формируют символ «1». В результате общее число символов «1» в любой передаваемой кодовой комбинации всегда будет чётным.
Таким образом, правило формирования проверочного символа cводится
к следующему:
r1 = i1 
i2 ... ik,
где i – соответствующий информационный символ (0 или 1); k – общее их число, а под операцией здесь и далее понимается сложение по модулю 2.
Очевидно, что добавление дополнительного разряда увеличивает общее число возможных комбинаций вдвое по сравнению с числом комбинаций исходного первичного кода, а условие чётности разделяет все комбинации на разрешённые и неразрешённые. Код с проверкой на чётность позволяет обнаруживать одиночную ошибку при приёме кодовой комбинации, так как такая ошибка нарушает условие чётности, переводя разрешённую комбинацию в запрещённую.
Критерием правильности принятой комбинации является равенство нулю результата S суммирования по модулю 2 всех n символов кода, включая проверочный символ ri. При наличии одиночной ошибки S принимает значение 1:
S = r1 i1 i2 ... ik = 0 – ошибки нет;
S = r1 i1 i2 ... ik = 1 – однократная ошибка.
Этот код является (k + 1, k) -кодом, или (n, n - 1)-кодом. Минимальное расстояние кода равно двум (dmin = 2), и, следовательно, никакие ошибки не могут быть исправлены. Простой код с проверкой на чётность может использоваться только для обнаружения (но не исправления) однократных ошибок.
Увеличивая число дополнительных проверочных разрядов и формируя по определённым правилам проверочные символы r, равные 0 или 1, можно усилить корректирующие свойства кода так, чтобы он позволял не только обнаруживать, но и исправлять ошибки. На этом и основано построение кодов Хемминга. Рассмотрим эти коды, позволяющие исправлять одиночную ошибку, с помощью непосредственного описания. Для каждого числа проверочных символов r = 3, 4, 5... существует классический код Хемминга с маркировкой
(n, k) = ( 2 r – 1, 2 r – 1 - r), (4.24)
т. е. – (7,4), (15,11), (31,26).
При других значениях числа информационных символов k получаются так
называемые усечённые (укороченные) коды Хемминга. Так, для международного телеграфного кода МТК-2, имеющего 5 информационных символов, потребуется использование корректирующего кода (9,5), являющегося усечённым от классического кода Хемминга (15,11), так как число символов в этом коде уменьшается (укорачивается) на 6. Для примера рассмотрим классический код Хемминга (7,4), который можно сформировать и описать с помощью кодера, представленного на рис. 4.2.
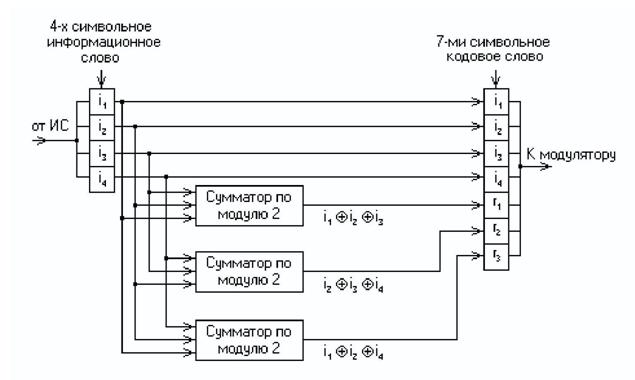
Рис. 4.2
В простейшем варианте при заданных четырёх (k = 4) информационных символах (i1, i2, i3, i4) будем полагать, что они сгруппированы в начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы тремя проверочными символами (r = 3), задавая их следующими равенствами проверки на чётность, которые определяются соответствующими алгоритмами
r1 = i1 i2 i3;
r2 = i2 i3 i4;
r3 = i1 i2 i4,
где знак «» означает сложение по модулю 2.
На рис. 4.3 приведена схема декодера для (7,4)-кода Хемминга, на вход которого поступает кодовое слово:
V = (i′ 1, i′ 2, i′ 3, i′ 4 , r′ 1, r′ 2, r ′ 3).
Апостроф означает, что любой символ слова может быть искажён помехой в канале передачи.
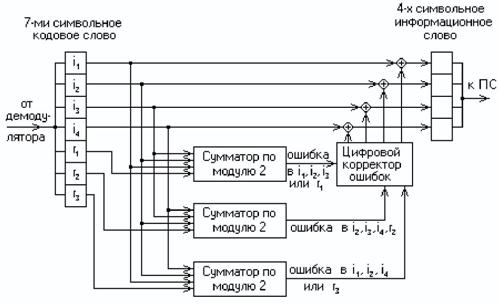
Рис. 4.3
В декодере, в режиме исправления ошибок, строится последовательность:
s 1 = r 1 ’ i 1 ’ i 2 ’ i 3’;
s 2 = r 2’ i 2’ i 3 ’ i 4 ’;
s 3 = r 3 ’ i 1 ’ i 2 ’ i 4’.
Трёхсимвольная последовательность (s 1, s 2, s 3 ) называется синдромом. Термин «синдром» используется и в медицине, где он обозначает сочетание признаков, характерных для определённого заболевания. В данном случае синдром S = (s 1, s 2, s 3 ) представляет собой сочетание результатов проверки на чётность соответствующих символов кодовой группы и характеризует определённую конфигурацию ошибок (шумовой вектор).
Кодовые слова кода Хемминга для k = 4 и r = 3 приведены в табл. 4.1.
Число возможных синдромов определяется выражением
S = 2 r. (4.25)
При числе проверочных символов r = 3, имеется восемь возможных синдромов (23 = 8). Нулевой синдром (000) указывает на то, что ошибки при приёме отсутствуют или не обнаружены. Всякому ненулевому синдрому соответствует определённая конфигурация ошибок, которая и исправляется. Классические коды Хемминга (4.20) имеют число синдромов, точно равное их необходимому числу, позволяют исправить все однократные ошибки в любом информативном и проверочном символах и включают один нулевой синдром. Такие коды называются плотноупакованными.
Таблица 4.1
| k = 4 | r = 3 | |||||
| i 1 | i 2 | i 3 | i 4 | r 1 | r 2 | r 3 |
Усечённые коды являются неплотноупакованными, так как число синдромов у них превышает необходимое. Так, в коде (9,5) при четырёх проверочных символах число синдромов будет равно 24 = 16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о неполной упаковке кода (9,5).
Для рассматриваемого кода (7,4) в табл. 4.2 представлены ненулевые синдромы и соответствующие конфигурации ошибок.
Таблица 4.2
| Синдром | |||||||
| Конфигурация ошибок | |||||||
| Ошибка в символе | r 3 | r 2 | i 4 | r 1 | i 1 | i 3 | i 2 |
Таким образом, код (7,4) позволяет исправить все одиночные ошибки. Простая проверка показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно создание такого цифрового корректора ошибок (дешифратора синдрома), который по соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе. После внесения исправления проверочные символы ri можно на выход декодера не выводить. Две или более ошибки превышают возможности корректирующего кода Хемминга, и декодер будет ошибаться. Это означает, что он будет вносить неправильные исправления и выдавать искажённые информационные символы.
Идея построения подобного корректирующего кода, естественно, не меняется при перестановке позиций символов в кодовых словах. Все такие варианты также называются (7,4) – кодами Хемминга.
