Пусть производятся испытания какого-либо изделия на безотказность работы. Вероятность отказа очень мала. В результате испытаний изделие не отказало ни разу. Найти максимальную, практически возможную, вероятность отказа.
Поставим эту задачу в общем виде. Произведено n независимых опытов, ни в одном из которых событие А не произошло. Задана доверительная вероятность b, требуется построить доверительный интервал для вероятности Р события А, точнее найти его верхнюю границу Р 2, так как нижняя граница Р 1 равна нулю.
В результате n опытов наблюдается противоположное событие В, состоящее в том, что событие А не появилось ни разу. Вероятность этого события определяется по формуле Бернулли при m = 0, где m – число появлений события В.

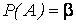 ,
, 
Получим уравнение для вероятности P 2:

откуда  . (3.70)
. (3.70)
Обратная задача.
Событие А с малой вероятностью ни разу не наблюдалось в серии из n опытов. Задана доверительная вероятность b. Каково должно быть число опытов, чтобы верхняя доверительная граница для вероятности события была равна заданному значению Р 2.
Из формулы (3.70) получим
 (3.71)
(3.71)






