Теоретические законы распределения случайных величин

В период нормальной эксплуатации постепенные отказы еще не проявляются и надежность характеризуется постоянными отказами. Эти отказы вызываются неблагоприятным стечением многих обстоятельств и поэтому имеют постоянную интенсивность, которая зависит от возраста изделия:

(4.1)

где – средняя наработка до отказа (обычно в часах). Тогда выражается числом отказов в час и, как правило, составляет малую дробь.

Вероятность безотказной работы

(4.2)

Она подчиняется экспоненциальному закону распределения времени безотказной работы и одинакова за любой одинаковый промежуток времени в период нормальной эксплуатации.

Экспоненциальным законом распределения можно аппроксимировать время безотказной работы широкого круга объектов (изделий): особо ответственных машин, эксплуатируемых в период после окончания приработки и до существенного проявления постепенных отказов; элементов радиоэлектронной аппаратуры; машин с последовательной заменой отказавших деталей; машин вместе с электро- и гидрооборудованием и системами управления и др.; сложных объектов, состоящих из многих элементов (при этом время безотказной работы каждого может не быть распределено по экспоненциальному закону; нужно только, чтобы отказы одного элемента, не подчиняющегося этому закону, не доминировали над другими).

Приведем примеры неблагоприятного сочетания условий работы деталей машин, вызывающих их внезапный отказ (поломку). Для зубчатой передачи это может быть действием максимальной пиковой нагрузки на наиболее слабый зуб при его зацеплении в вершине и при взаимодействии с зубом сопряженного колеса, при котором погрешности шагов сводят к минимуму или исключают участие в работе второй пары зубьев. Такой случай может встретится только через много лет эксплуатации или не встретится совсем.

Примером неблагоприятного сочетания условий, вызывающего поломку вала, может явится действие максимальной пиковой нагрузки при положении наиболее ослабленных предельных волокон вала в плоскости нагрузки.

Существенное достоинство экспоненциального распределения – его простота: оно имеет только один параметр.

Если, как обычно, то формула для вероятности безотказной работы упрощается в результате разложения в ряд и отбрасывания малых членов:

 

(4.3)

Плотность распределения (в общем случае)

 

(4.4)

 

Значения вероятности безотказной работы в зависимости от (рис. 4.1):

 

 

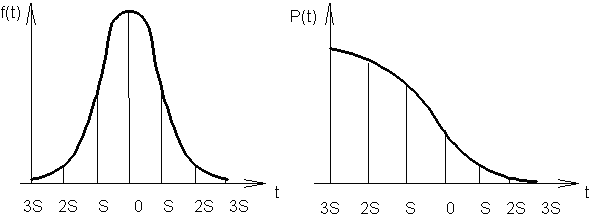
Рис.4.1. Графики плотности распределения и вероятности безотказной работы

 

Таблица 4.1

Значения вероятности безотказной работы в зависимости от интенсивности отказов

		0,1	0,01	0,001	0,0001
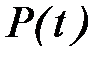
	0,368	0,9	0,99	0,999	0,9999

 

Так как при вероятность , то 63% отказов возникают за время и только 37% позднее. Из приведенных значений следует, что для обеспечения требуемой вероятности безотказной работы 0.9 или 0.99 можно использовать только малую долю среднего срока службы (соответственно 0.1 и 0.01).

Если работа изделия происходит при разных режимах, а следовательно, и интенсивностях отказов (за время ) и (за время ), то

(4.5)

Эта зависимость следует из теоремы умножения вероятностей. Для определения на основании опытов интенсивности отказов оценивают среднюю наработку до отказа

 

(4.6)

где N –общее число наблюдений. Тогда

Можно также воспользоваться графическим способом: нанести экспериментальные точки в координатах и

Знак минус выбирают потому, что и, следовательно - отрицательная величина

Тогда, логарифмируя выражение для вероятности безотказной работы:

 

(4.7)

заключаем, что тангенс угла прямой, проведенной через экспериментальные точки, равен

(4.8)

откуда

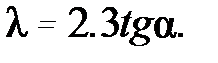(4.9)

При этом способе нет необходимости доводить до конца испытания всех образцов.

Вероятностная бумага (бумага со шкалой, в которой кривая функции распределения изображается прямой) должна иметь для экспоненциального распределения полулогарифмическую шкалу.

Для системы

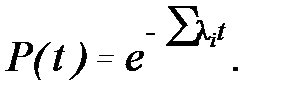(4.10)

Если

то

(4.11)

Таким образом, вероятность безотказной работы системы, состоящей из элементов с вероятностью безотказной работы подчиняющихся экспоненциальному закону, также подчиняется экспоненциальному закону, причем интенсивности отказов отдельных элементов складываются.

Используя экспоненциальный закон распределения, несложно определить среднее число изделий n, которые выйдут из строя к заданному моменту времени, и среднее число изделий N, которые останутся работоспособными. При

 

(4.12)

 

В связи с многообразием причин и условий возникновения постепенных отказов в этот период для описания надежности применяют несколько законов распределений, которые устанавливают путем аппроксимации результатов испытаний или наблюдений в эксплуатацию.

Нормальное распределение является наиболее универсальным, удобным и широко применяемым для практических расчетов.

Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие примерно равнозначные факторы.

Нормальному распределению подчиняется наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий, размеры и ошибки измерений деталей и т. д.

Плотность распределения

(4.13)

Распределение имеет два независимых параметра: математическое ожидание и среднее квадратическое отклонение S. Значения параметров и S оценивают по результатам испытания по формулам

(4.14)

 

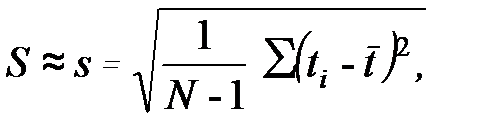(4.15)

где и s - оценки математического ожидания и среднего квадратического отклонения.

Сближение параметров и их оценок увеличивается с увеличением числа испытаний.

Иногда удобнее оперировать с дисперсией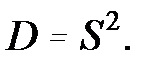

Математическое ожидание определяет на графике положение петли, а среднее квадратическое отклонение - ширину петли.

Кривая плотность распределения тем острее и выше, чем меньше S. Она начинается от и распространяется до . Это не является существенным недостатком, особенно если так как площадь, очерченная уходящими в бесконечность ветвями кривой плотности, выражающая соответствующую вероятность отказов, очень мала. Так, вероятность отказа за период времени до составляет всего 0.135% и обычно не учитывается в расчетах. Вероятность отказа до равна 2.175%. Наибольшая ордината кривой плотности распределения равно .

Интегральная функция распределения

(4.16)

Вычисление интегралов заменяют использованием таблиц. Таблицы для нормального распределения в функции и S были бы громоздкими, так как имели бы два независимых параметра. Можно обойтись небольшими таблицами для нормального распределения, у которого и . Для этого распределения функция плотности

; (4.17)

имеет одну переменную x. Величина x является центрированной, так как , и нормированной, так как . Функция плотности распределения записывается в относительных координатах с началом на оси симметрии петли.

Функция распределения - интеграл от плотности распределения

(4.18)

Из этого уравнения следует, что

(4.19)

отсюда

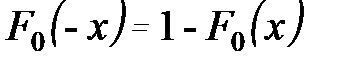. (4.20)

Для использования таблиц следует применить подстановку

(4.21)

при этом x называется квантилью нормированного нормального распределения и обычно обозначается

Плотность распределения и вероятность безотказной работы соответственно

 

где и берут по таблицам.

 

Таблица 4.2

Значения функции распределения в зависимости от плотности распределения

x
	0,3989	0,2420	0,0540	0,0044	0,0001
	0,5	0,8413	0,9772	0,9986	0,9999

 

В таблице 4.1. приведены непосредственно значения в зависимости от 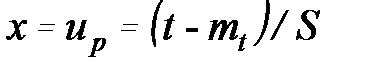в употребительном диапазоне.

В литературе по надежности часто вместо интегральной функции распределения пользуются функцией Лапласа:

(4.22)

Очевидно, что

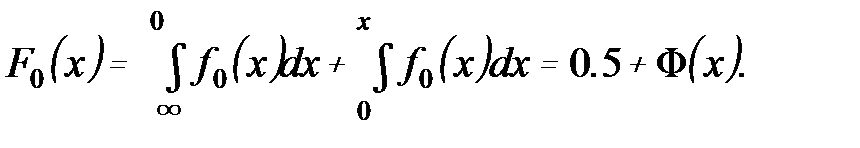(4.23)

Вероятность отказа и вероятность безотказной работы, выраженные через функции Лапласа, отличаются пределами интегрирования, имеют вид:

(4.24)

(4.25)

Сравнивая изделия с одинаковой средней наработкой до отказа и разным средним квадратическим отклонением S, нужно подчеркнуть, что хотя при больших S и имеются экземпляры с большой долговечностью, но чем меньше S, тем много лучше изделие.

Помимо задачи оценки вероятности безотказной работы за данное время или за данную наработку встречается обратная задача - определение времени или наработки, соответствующих заданной вероятности безотказной работы.

Значение этой наработки (времени) определяют с помощью квантилей нормального распределения

Значения квантилей даются в таблице в зависимости от требуемой вероятности, в частности от вероятности безотказной работы.

 

Таблица 4.3

Значения вероятности безотказной работы в зависимости от квантили

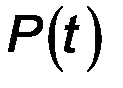
	0,5	0,90	0,95	0,99	0,999	0,9999
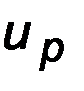
		-1,282	-1,645	-2,326	-3,090	-3,719

 

Операции с нормальным распределением проще, чем с другими, поэтому им часто заменяют другие распределения. При малых коэффициентах вариации нормальное распределение хорошо заменяет биномиальное, пуассоново и логарифмически нормальное.

Распределение суммы независимых случайных величин, называемое

 

(4.26)

композицией распределений, при нормальном распределении слагаемых также является нормальным распределением.

Математическое ожидание и дисперсия композиции соответственно равны

(4.27)

(4.28)

 

где 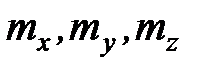- математические ожидания случайных величин X, Y, Z; –дисперсия тех же величин.

Влогарифмически нормальном распределении логарифм случайной величины распределяется по нормальному закону. Как распределение положительных величин, оно несколько точнее, чем нормальное, описывает наработку деталей, в частности, по усталости. Его успешно применяют для описания наработки подшипников качения, электронных ламп и других изделий.

Логарифмически нормальное распределение удобно для случайных величин, представляющих собой произведение значительного числа случайных исходных величин, подобно тому как нормальное распределение удобно для суммы случайных величин.

Плотность распределения описывается зависимостью

(4.29)

 

где и S –параметры, оцениваемые по результатам испытаний.

Так, при испытаниях N изделий до отказа

(4.30)

; (4.31)

Вероятность безотказной работы можно определить по таблицам для нормального распределения (см. табл. 4.3) в зависимости от значения квантилей

Математическое ожидание наработки до отказа

(4.32)

среднее квадратическое отклонение

(4.33)

коэффициент вариации

(4.34)

При полагают при этом ошибка меньше или равна 1%.

Распределение Вейбулла довольно универсально, охватывает путем варьирования параметров широкий диапазон случаев изменения вероятностей. Наряду с логарифмически нормальным распределением оно удовлетворительно описывает наработку деталей по усталостным разрушениям, наработку до отказа подшипников, электронных ламп. Используется для оценки надежности деталей и узлов машин, в частности, станков, подъемно-транспортных и других машин. Применяется также для оценки надежности по приработочным отказам.

Распределение характеризуется следующей функцией вероятности безотказной работы:

(4.35)

 

Интенсивность отказов

(4.36)

Плотность распределения

 

. (4.37)

Распределение Вейбулла имеет также два параметра: параметр формы m > 0 и параметр масштаба

Математическое ожидание и среднее квадратическое отклонение соответственно

(4.38)

; (4.39)

где и 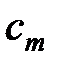- коэффициенты.