Основные зависимости надежности при постоянных и внезапных отказах

 

Внезапные отказы определяются случайными неблагоприятными сочетаниями нескольких факторов. Случайность связана с тем, что причины события остаются для нас скрытыми. Рассеяние ресурсов по критерию усталости (оцениваемое отношением наибольшего ресурса к наименьшему) для подшипников достигает 40, для зубчатых передач 10...15. Рассеяние ресурсов по износу также весьма значительно. Существенное рассеяние имеют действующие нагрузки, механические характеристики материалов и деталей, зазоры и натяги, которые при изготовлении получаются как разности сопрягаемых размеров.

Поэтому в расчетах надежности многие параметры должны рассматриваться случайными величинами, т. е. такими, которые могут принять то или иное значение, неизвестное заранее. Они могут быть непрерывного или дискретного (прерывного) типа.

Для каждого числа x в диапазоне изменения случайной величины X существует определенная вероятность P (X < x), что X не превосходит x. Эта зависимость F(x)=P(X<x) называется функцией распределения или функцией вероятности случайной величины X.

Функция F(x) является неубывающей функцией x (монотонно возрастающей для непрерывных процессов и ступенчато возрастающей для дискретных процессов). В пределах изменения случайной величины X она изменяется от 0 до 1.

Производная от функции распределения по текущей переменной 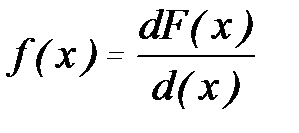называется плотностью распределения. Она характеризует частость повторений данного значения случайной величины. В задачах надежности она широко используется как плотность вероятности.

В ряде случаев достаточно характеризовать распределение случайной величины некоторыми числовыми величинами: математическим ожиданием (средним значением), модой и медианой, характеризующими положение центров группирования случайных величин по числовой оси, дисперсией, средним квадратическим отклонением, коэффициентом вариации, характеризующим рассеяние случайной величины. Характеристики распределений используются в статистической трактовке (для обработки результатов наблюдений) и в вероятностной трактовке (для прогнозирования надежности).

Математическое ожидание (среднее значение) m_x – основная и простейшая характеристика случайной величины x. Значение математического ожидания, определяемое по результатам наблюдений как для дискретных, так и для непрерывных величин, называют оценкой математического ожидания или оценкой среднего значения :

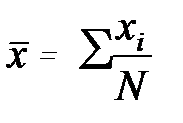или 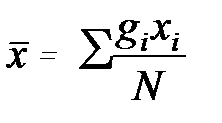, (3.1)

где N –общее число наблюдений;

x_i - значение случайной величины;

g_i - число одинаковых значений x_i.

Черта над обозначением случайной величины означает среднее значение.

В первой формуле суммируют все N члены, во второй - число членов с разными значениями x_i. При достаточно большом числе наблюдений (испытаний) полагают, что m_x= .

В вероятностных задачах математическое ожидание определяют в зависимости от плотности распределения f(x) (для непрерывных величин) или вероятности p_i появления значения x_i (для дискретных величин):

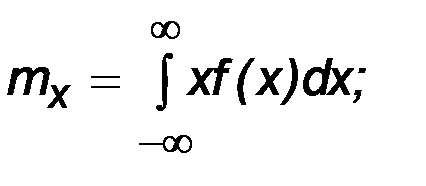
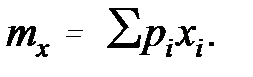(3.2)

Дисперсия случайной величины - математическое ожидание квадрата отклонения этой величины от ее математического ожидания.

Оценка дисперсии случайной величины - среднее значение квадрата разности между значениями случайной величины и ее средним значением:

, или (3.3)

D^*_x = 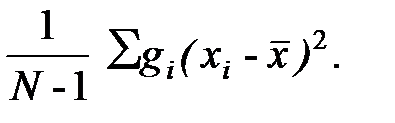(3.4)

Слово дисперсия означает рассеяние и характеризует разброс случайной величины.

Для непрерывных случайных величин

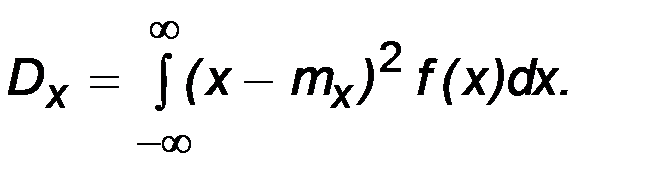(3.5)

Для дискретных случайных величин

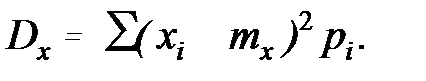(3.6)

Дисперсия имеет размерность квадрата случайной величины. Так как удобнее пользоваться характеристикой рассеяния, имеющей ту же размерность, что и случайная величина, то была введена характеристика – среднее квадратическое отклонение, представляющее собой корень квадратный из дисперсии, т.е.

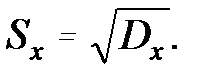(3.7)

Для оценки рассеяния с помощью безразмерной (относительной) величины используют коэффициент вариации, равный отношению среднего квадратического отклонения к математическому ожиданию, т.е.

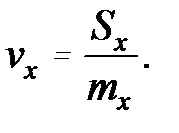(3.8)

Дисперсия и среднее квадратическое отклонение являются гораздо более представительными характеристиками рассеяния, чем, например, среднее арифметическое абсолютных значений отклонений.

Квантилью называют значение случайной величины, соответствующее заданной вероятности.

Квантиль, соответствующая вероятности 0,5 называется медианой. Медиана характеризует расположение центра группирования случайной величины. Площадь под графиком функции плотности распределения делится медианой пополам.

Для характеристики рассеяния случайной величины используют также вероятное отклонение, равное половине разности квантилей x_0,75 и x_0,25 т. е. значение случайной величины соответствующих вероятностям 0,75 и 0,25.

Модой случайной величины называется ее наиболее вероятное значение или, иначе, то ее значение, при котором плотность вероятности максимальна.