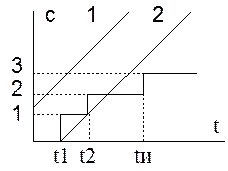
Пусть испытывается выборка из N изделий. Результаты можно представить в виде графика. В результате испытаний получаем ступенчатую линию которую можно рассматривать как некоторую случайную реализацию случайного процесса появления отказов в выборке. Каждая ступенька соответствует 1 отказу. При одноступенчатом и двухступенчатом контроле заключение о надежности делается по истечении времени испытаний Ти, и по общему итогу испытаний R, которое сравнивается с предельным числом отказов С. Если ступенчатая линия пересечет вертикаль ниже – С, то результат испытаний положителен.
При последовательном контроле проверка надежности делается после каждого испытания. Для заданных Q0 (вероятность отказа), Q1 (браковочный уровень), риск поставщика), риск заказчика) по специальным формулам строятся 2 параллельные кривые (1 – линия соответствия, 2 – линия несоответствия). Если в момент отказа ступенчатая линия ниже линии 1, то принимается решение о надежности. Если ступенчатая линия выше линии 1, но ниже 2, то испытания продолжаются. Если ступенчатая линия выше 2, то принимается решение о несоответствии.

20. ТОЧЕЧНАЯ И ИНТЕРВАЛЬНАЯ ОЦЕНКА ПАРАМЕТРОВ НАДЁЖНОСТИ. ТОЧЕЧНАЯ И ИНТЕРВАЛЬНАЯ ОЦЕНКА КРИТЕРИЕВ НАДЁЖНОСТИ. ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ И ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ.
Ранее мы получали оценки, которые являются точечными и не являются абсолютно точечными. Истинное значение может быть как меньше так и больше точечных оценок. Поэтому правильнее было бы узнать интервал, в пределах которого заключено истинное значение. Совершенно очевидно, что как бы широк этот интервал не был (в разумных пределах) утверждать со 100 % вероятностью, что истинное значение заключается в нем утверждать нельзя. Можно говорить об этом с той или иной долей вероятности. Например: с вероятность 0,9 можно утверждать, что продолжительность жизни человека находится в интервале между 65 и 75 годами, а с вероятностью 0,99 между 50 и 80 годами. Рассмотрим способы определения доверительных интервалов и критерий доверия, то есть вероятность того, что рассмотренный параметры заключен в указанных параметрах. Если из совокупности N взять несколько выборок. n1,n2,…nk, и для каждой выборки определить Тср1,Тср2,…Тсрк, то все они будут разными.Причем отклонения от Тср будут распределены нормальным законом. Параметры закона по статистической совокупности определяется по следующим формулам. Тср*= i=1∑n ti/n
S*=√i=1∑n(ti-Tcp)/n-1, Где S* несмешанная оценка.
Стандартное отклонение σ=√ i=1∑n (ti-Tcp)2 / n. Получаемое значение из ряда выработок опред по след выр: σ (Тср) = σ*/√n, где n- число отказов. Приведенные выражения позволяют непосредственно определить доверительный интервал. Для этого необходимо знать Тср и σ.
 При числе отказов от 20-30 принять что Тср = Тср*, σ = S*
При числе отказов от 20-30 принять что Тср = Тср*, σ = S*
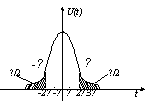
Если мы зададимся доверительной вертикалью, то есть площадью под кривой, то можем определить доверительный интервал. И наоборот, задавшись шириной интервала, можно определить коэффициент доверия.
Установлено, что доверительной интервал будет минимальный, если площадь под кривой плотности распределения U(t) в интервале
(-∞;-2σ(-kα/2)][2σ(kα/2);+∞) будет равны. И если обозначить максимальное отклонение через Е то ширина интервала будет равна Тср±ε, а критерий доверия
Р{Тср*–ε≤Тср≤Тср*+ε}=1-α. Вычисления критерия доверия, то есть вероятность взятой по обычной методике(по таблице интервала вероятности или функции Лапласа)
γ=1- α =Ф[ε/ σ (Тср)] =Ф[(ε √n)/S*] =2Фо(Z), Фо–нормированное, центрированное значение. Данная задача может решаться в двух вариантах: 1)опред по заданному критерию доверительных интервалов;2) по заданным доверительным интервалам вычисл критерий доверия
Для 1) Е=Z*S*/√n;Z=(E√n)/s*






