Положим, что Z 1 и Z 2 в схемах (рис.3.8) подобраны так, что Z 1ВХ= Z 1, Z 2ВХ= Z 2. Иначе говоря, что существуют два сопротивления Z 1= Z 1С и Z 2= Z 2С, которые удовлетворяют следующему условию: входное сопротивление Z 1ВХ четырехполюсника нагруженного на Z 2С равно Z 1С. Входное сопротивление четырехполюсника Z 2ВХ, нагруженного на Z 1С равно Z 2С.
Такие два сопротивления (Z 1С и Z 2С) называют характеристическими сопротивлениями несимметричного четырехполюсника.
Условие, когда четырехполюсник нагружен соответствующим характеристическим сопротивлением, называется условием согласованной нагрузки или согласованного включения.
Положив в (3.10) и (3.11) Z 1ВХ= Z 1С, Z 2ВХ= Z 2С получим:
, 
.
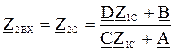Совместное решение этих уравнений относительно Z 1С и Z 2С дает:
; 
. (3.12)
Введем для рассматриваемого взаимного четырехполюсника параметр g, удовлетворяющий условию:
chg= 
, (3.13)
shg= 
. (3.14)
Коэффициент g в общем случае – комплексный. Кроме, того эти условия взаимно дополняют друг друга, так как AD - BC =1.
Положим g=a+jb. Он называется коэффициентом передачи. Действительная часть «а» называется собственным затуханием четырехполюсника, а мнимая часть «b» - коэффициентом фазы.
Выразим коэффициенты А-формы четырехполюсника через характеристические параметры.
Из (3.12)
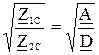, (3.15)
. (3.16)
Используя (3.13), (3.14), (3.15), (3.16) получим:
chg, 
shg, 
chg, 
shg.
После подстановки коэффициентов в А-форму записи четырехполюсника имеем:
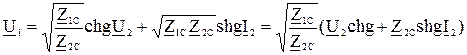, (3.17)
. (3.18)
При согласованной нагрузке Z 2= Z 2C; U 2= I 2 Z 2 и уравнения (3.17) и (3.18) примут вид:
, (3.19)
. (3.20)
Модули напряжений и токов связаны выражением:
, (3.21)
. (3.22)
В свою очередь:
; 
.
Используя уравнения (3.19) и (3.20), получим 
; 
.
В случае симметричного четырехполюсника A = D и 
.
Следовательно входное сопротивление четырехполюсника, нагруженного на Z C равно Z С. Это означает, что
.
На основании (3.17) и (3.18) уравнение симметричного четырехполюсника имеет вид в гиперболической форме:
(3.24)
Откуда 
; Амплитудные изменения напряжения и тока определяются множителем еа.
.
Собственное затухание «а» вычисляют в белах (Б) или децибелах (дБ), которые определяются следующим образом: если полная мощность на выходе четырехполюсника в 10 раз меньше мощности на его входе, то затухание составляет 1 Б, если мощность уменьшается в 100 раз, то затухание оценивается в 2 Б и т.д. Поэтому
аБ=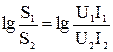 
.
В случае согласованного нагруженного симметричного четырехполюсника:
.
Следовательно аБ=2 
.
Децибел – единица, в 10 раз меньшая бела. Затухание в 1 дБ соответствует уменьшению полной мощности в 1,26 раза или уменьшению напряжения и тока в 1,2 раза.
Затуханию 1 Нn соответствует уменьшению амплитуды и действующего значения напряжения и тока в е раз так как при 
имеем 
1дБ=0,115 Hn,
1Hn=8,686 дБ.
