Для того, чтобы коэффициенты одной формы записи найти через коэффициенты другой формы записи, необходимо выделить одинаковые величины и сопоставить их, учтя направление токов I 1 и I 2.
Например, определим соотношение между коэффициентами А и Н формы записи четырехполюсников.
А-форма:
 (3.7)
(3.7)
Н-форма:
 (3.8)
(3.8)
Из (3.7) определим:
 ;
;  .
.
Учтем, что:
I 2(H)=- I 2(A)
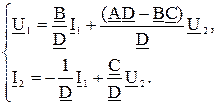 (3.9)
(3.9)
Сопоставим (3.8) и (3.9), тогда:
 ;
;  ;
;  ;
;  .
.
В частном случае между коэффициентами четырехполюсников, могут существовать те или иные зависимости. Между параметрами взаимных четырехполюсников существуют следующие зависимости:
Z 12= Z 21; Y 12= Y 21; H 12=- H 21; G 12=- G 21; AD - BC =1; В12¹В21 даже по модулю.
Итак взаимные четырехполюсники характеризуются не более чем тремя независимыми параметрами.
Симметричные четырехполюсники характеризуются лишь двумя независимыми параметрами, поскольку они по определению взаимны и у них кроме того,
Z 11= Z 22; Y 11= Y 22; H 11 H22 - H 12 H 21=1; G 11 G 22- G 12 G 21=1; A = D.
3.4. Т и П – СХЕМЫ ЗАМЕЩЕНИЯ ПАССИВНОГО ЧЕТЫРЕХПОЛЮСНИКА
Функции пассивного взаимного четырехполюсника, как передаточного звена между источником и нагрузкой может выполнять Т-схема (рис. 3.5,а) или эквивалентная ей П-схема (рис.3.5, б)
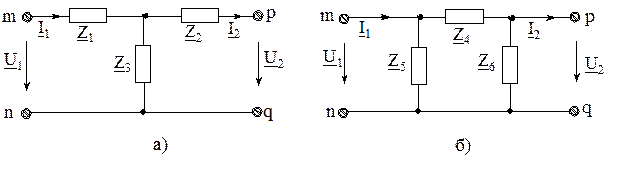
Рис.3.5. Т-схема и П-схема пассивного четырёхполюсника
Сопротивления Т и П-схемы подсчитываются с учетом того, что схема замещения должна обладать теми же коэффициентами A, B, C, D, что и заменяемый ее четырехполюсник.
Покажем как определяются параметры Z 1, Z 2, Z 3 Т-схемы замещения по известным коэффициентам A, B, C, D, четырехполюсника.
Выразим напряжение U 1 и ток I 1, через U 2 и I 2.
 ,
,
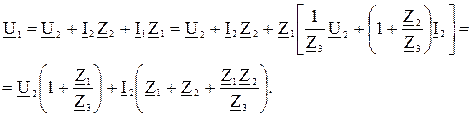
Сравнивая полученные выражения с А-формой, находим, что:
 ;
;  ;
;  ;
;  ;
;
следовательно:
 ;
;  ;
;  .
.
Эти формулы позволяют определить сопротивление Т-схемы замещения по известным коэффициентам A, B, C, D, четырехполюсника.
Если четырехполюсник симметричный, то A=D и Z 1= Z 2. Аналогичным образом определяют Z 4, Z 5, Z 6 для П схемы.






