Число сочетаний из четырех по два (U 1, U 2, I 1, I 2) равно шести, поэтому возможны следующие шесть форм записи:
А – форма:
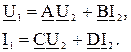
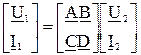 .
.
Y – форма:
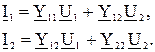
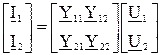 .
.
Z – форма:
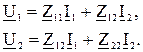
 .
.
H – форма:
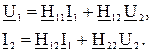
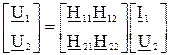 .
.
G – форма:
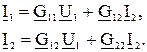
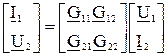 .
.
В – форма:
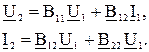
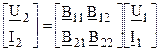 .
.
Исторически сложилось так, что для А-формы направление токов и напряжений соответствует рис.3.1,а - для Y и Z- формы; Н и G- формы – рис.3.1,б; для В- формы рис.3.1,в.
Для изучения теории и исследование режимов четырехполюсников, выведем уравнение А-формы записи четырехполюсников.
Напряжение на нагрузке U 2= I 2 Z 2 (рис.3.2).

Рис.3.2. Схема четырёхполюсника с нагрузкой
На основании теоремы о компенсации Z 2 можно заменить на E 2= I 2 Z 2 (Е2 – направлена против тока (рис.3.3))

Рис.3.3. Замена сопротивления нагрузки на Э.Д.С.
По принципу наложения:
 (3.1)
(3.1)
В этих уравнениях взято «- Е 2», так как оно направлено против токов, созданных Е 1. Напряжение U 1= E 1, U 2= E 2, тогда в (3.1):
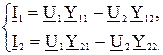 (3.2)
(3.2)
Из уравнений (3.2):
 (3.3)
(3.3)
или:
 (3.4)
(3.4)
Коэффициенты четырехполюсника (взаимного) связаны соотношением:
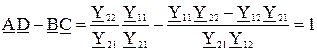 .
.
Их значения зависят только от величин сопротивлений и конфигурации четырехполюсника.
Если в схеме рис.3.2 поменять местами источник и нагрузку, и изменить положительные направления токов I 1 и I 2 (рис.3.4), то уравнение (3.4) примет
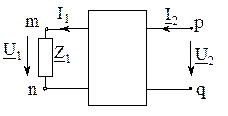
Рис.3.4. Схема четырёхполюсника при изменении мест включения источника и нагрузки
вид:
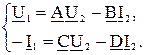 (3.5)
(3.5)
Из уравнения (3.5) с учетом, что AD – BC =1 получим:
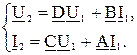 (3.6)
(3.6)
Сравнивая (3.4) и (3.6) легко заметить, что при замене первичных зажимов вторичными коэффициенты А и D меняются местами.
Уравнение симметричного четырехполюсника должно в данном случае остаться неизменным. Поэтому у симметричного четырехполюсника A=D. Все четырехполюсники не удовлетворяющие этому условию являются несимметричными.






