Задание 1. Даны два множества: 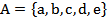 и
и  . Найти соответствие между записями:
. Найти соответствие между записями:  ,
,  ,
,  ,
,  .
.
1). 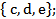 2).
2).  ; 3).
; 3). 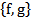 ; 4).
; 4).  .
.
Задание 2. Заданы произвольные множества  ,
,  ,
,  . Расположите указанные справа множества так, чтобы каждое из них было подмножеством следующего за ним.
. Расположите указанные справа множества так, чтобы каждое из них было подмножеством следующего за ним.
1).  2).
2).  ; 3).
; 3).  ; 4).
; 4).  .
.
Задание 3. Заданы множества  и
и  . Тогда декартовым произведение этих множеств
. Тогда декартовым произведение этих множеств  является множество:
является множество:
1)  2).
2).  ; 3).
; 3).  ; 4).
; 4). 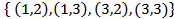 .
.
Задание 4. В корзине лежат белые шары, раскрашенные разными полосками: красными, синими и зелеными. Красные полоски имеют 12 шаров, синие полоски есть на 10 шарах, а зеленые полоски нарисованы на 8 шарах. Красные и синие полоски встречаются на 6 шарах, красные и зеленые полоски мелькают на 4 шарах, а синие и зеленые полоски расположены на 2 шарах. Полоски трех цветов нарисованы только на одном шаре. Сколько всего шаров в корзине? Сколько шаров имеют только красные полоски? Сколько шаров имеют только синие полоски? Сколько шаров имеют только зеленые полоски?
Задание 5. На вещественной плоскости  начертите фигуры, изображающие множества
начертите фигуры, изображающие множества
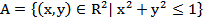 и
и  . Какие фигуры изображают множества
. Какие фигуры изображают множества  ,
,  ,
,  ?
?
Задание 6. Сколько простых чисел в диапазоне от 2 до 100?
Задание 7. Показать при помощи диаграмм Эйлера-Венна, какие равенства из перечисленных ниже верны для любых множеств  ,
,  ,
,  .
.
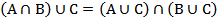
| |

| |

| |

| |

| |

|
Задание 8. Используя основные определения и законы теории множеств, доказать следующие тождества:

| |

| |

| |

|
[1] Два целых числа  и
и  сравнимы по модулю натурального числа
сравнимы по модулю натурального числа  , если при делении на
, если при делении на  они дают одинаковые остатки
они дают одинаковые остатки  . Число
. Число  называется модулем сравнения.
называется модулем сравнения.






