ћножества. ќсновные пон€ти€
ѕон€тие множества €вл€етс€ основным, неопредел€емым пон€тием, поэтому можно только по€снить этот термин. ѕод множеством  понимаетс€ собрание определенных и различимых между собой объектов, мыслимое как единое целое.
понимаетс€ собрание определенных и различимых между собой объектов, мыслимое как единое целое.
¬ этом интуитивном определении, принадлежащем немецкому математику √еоргу антору (1845-1918), существенным €вл€етс€ то обсто€тельство, что собрание предметов само рассматриваетс€ как один предмет. „то касаетс€ самих предметов, которые вход€ во множество, то относительно них существует значительна€ свобода. Ёто может быть и множество целых чисел, и множество точек на плоскости и множество белых носорогов. ћножество не об€зательно должно содержать в каком-то смысле однородные объекты. ћожно объединить в одном множестве и множество объектов и его одиночных представителей.
ћножества обычно обозначаетс€ заглавными латинскими буквами A, B, C,Е. ћножество можно задать списком, перечислив все его элементы:
ѕри этом пор€док, в котором элементы расположены при описании множества, не имеет значени€. Ќе имеет значени€ также возможность неоднократного повторени€ одних и тех же элементов при описании множества. | |||

| |||
| √еорг ‘ердинанд Ћюдвиг ‘илипп антор |
другому способу задани€ множества можно отнести порождающую процедуру, например,

| (1.2) |
¬ данном случае под выражением  можно понимать арифметические операции, или некоторые неформальные описани€.
можно понимать арифметические операции, или некоторые неформальные описани€.
ѕример. ћножество  содержит один элемент:
содержит один элемент:  состоит из набора элементов
состоит из набора элементов  .
.
ќпределение множества, как совокупности всех неких объектов, которые обладают неким заданным нам свойством, не всегда может привести к однозначному ответу.
ѕример ѕарадокс –ассела. ¬ладелец парикмахерской в одном селе повесил следующее объ€вление: ЂЅрею тех и только тех жителей села, кто не бреетс€ самї. —прашиваетс€, кто бреет брадобре€?
Ётот парадокс свидетельствует о том, что широко используема€ теори€ множеств в ее интуитивном, Ђнаивномї изложении €вл€етс€ противоречивой. ‘ормализаци€ теории множеств, св€занна€, в частности, с устранением парадоксов, способствовала развитию не только методов теории множеств, но и такой науки, как математическа€ логика.
—имволом  обозначаетс€ отношение принадлежности. «апись
обозначаетс€ отношение принадлежности. «апись  означает, что элемент
означает, что элемент  €вл€етс€ элементом множества
€вл€етс€ элементом множества  .
.
ќпределение 1.1. ћножества  и
и  считаютс€ равными, если они состо€т из одних и тех же элементов.
считаютс€ равными, если они состо€т из одних и тех же элементов.
«аписать утверждение о том, что множество  равно множеству
равно множеству  можно при помощи простой формулы
можно при помощи простой формулы

| (1.3) |
≈сли множества состо€т из разных элементов, то этот факт записывают

| (1.4) |
ѕример ƒаны три множества  ,
,  и
и  . ¬ силу того, что все три множества состо€т из одних и тех же элементов, справедлива запись
. ¬ силу того, что все три множества состо€т из одних и тех же элементов, справедлива запись  .
.
ѕример 1.2. ƒаны два множества  и
и  . Ёти множества нельз€ считать равными, так как единственным элементом множества
. Ёти множества нельз€ считать равными, так как единственным элементом множества  есть множество
есть множество 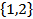 , множество
, множество  состоит из двух элементов: чисел 1 и 2.
состоит из двух элементов: чисел 1 и 2.
ќпределение 1.2. ≈сли все элементы множества ј принадлежат также множеству ¬, причем  , то множество ј €вл€етс€ подмножеством ¬. Ётот факт обозначают так:
, то множество ј €вл€етс€ подмножеством ¬. Ётот факт обозначают так:
|
|
|
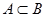
| (1.5) |
ќпределение 1.3. ≈сли каждый элемент множества ј есть элемент множества ¬, причем возможно  , то множество ¬ включает подмножеством ј:
, то множество ¬ включает подмножеством ј:

| (1.6) |
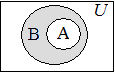
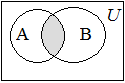
ƒл€ нагл€дного представлени€ отношений между подмножествами какого-либо универсального множества используютс€ диаграммы ¬енна. ѕростые и лаконичные рисунки, которые впервые предложил английский математик ƒжон ¬енн (1834-1923), используютс€ дл€ иллюстрации взаимосв€зей и в теории веро€тности, и в логике, и в статистике и в информатике.
¬ теории множеств сами множества обозначают област€ми и размещают внутри пр€моугольника, который представл€ет собой некое универсальное множество  . ≈сли два множества имеют общие элементы, то такие объекты иллюстрируютс€ перекрывающимис€ област€ми. . ≈сли два множества имеют общие элементы, то такие объекты иллюстрируютс€ перекрывающимис€ област€ми.
| 
|
| ƒжон ¬енн |
ѕример 1.5. ƒаны два множества  , и , и  . ƒл€ этих множеств справедливо . ƒл€ этих множеств справедливо  , поскольку множество , поскольку множество  включает множество включает множество  , и каждый элемент множества , и каждый элемент множества  есть элемент множества есть элемент множества  . .
| 
|
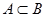
|
ћножество, не содержащее элементов, называетс€ пустым, и обозначаетс€ символом Ø. ѕустое множество есть подмножество любого множества.
ћножества бывают конечные и бесконечные. онечные множества содержат конечное число элементов. ћножества, не €вл€ющиес€ конечными, называютс€ бесконечными.
„исло элементов конечного множества называетс€ его мощностью. ћощность множества  обозначают
обозначают  .
.
ѕример 1.6. ƒано множество  . “огда
. “огда  =5.
=5.
ћножество всех подмножеств множества  называетс€ множеством-степенью и обозначаетс€
называетс€ множеством-степенью и обозначаетс€  . ≈сли множество
. ≈сли множество  состоит из
состоит из  элементов, то множество
элементов, то множество  состоит из
состоит из 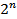 элементов.
элементов.
ѕример 1.7. ƒано множество 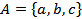 . ћножество-степень содержит следующие подмножества:
. ћножество-степень содержит следующие подмножества:
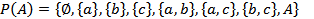
ќперации над множествами
–ассмотрим методы получени€ новых множеств их уже существующих.
ќпределение 1.4. ѕересечением множеств ј и ¬ называетс€ множество —, состо€щее из всех элементов, одновременно вход€щих и в множество ј, и во множество ¬. Ёто записываетс€ следующим образом:

| (1.3) | |
—войства операции пересечени€ множеств:
1.  (коммутативность);
2. (коммутативность);
2.  (ассоциативность);
3. (ассоциативность);
3.  ;
4. ;
4. 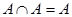 ;
5. ;
5.  Ø = Ø. Ø = Ø.
| 
| |

| ||
ѕример 1.7. ≈сли множество ј есть интервал (1; 5) а множество ¬ есть интервал (2; 7), то пересечение множеств ј и ¬ есть интервал (2; 5):  .
.
ќпределение 1.5. ќбъединением множеств ј и ¬ называетс€ множество —, состо€щее из всех элементов, каждый из которых принадлежит хот€ бы одному из данных множеств или ј, или ¬, или ј и ¬ одновременно. Ёто обозначаетс€ следующим образом:

| (1.4) | |
—войства операции объединени€ множеств:
1.  (коммутативность);
2. (коммутативность);
2.  (ассоциативность);
3. (ассоциативность);
3.  (дистрибутивность);
4. (дистрибутивность);
4.  ;
5. ;
5. 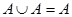 ;
6. ;
6.  Ø = Ø. Ø = Ø.
| 
| |
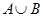
| ||
ѕример 1.8. ≈сли множество ј есть отрезок [1; 3] а множество ¬ есть отрезок [2; 5], то объединение множеств ј и ¬ есть отрезок [1; 5]:  .
.
ќпределение 1.6. ƒополнением множества ј называетс€ множество всех элементов универсального множества U, каждый из которых не принадлежит множеству ј.
ƒополнение множества ј будем обозначать через 
—войства операции дополнени€ множеств:
| 
|

|
ѕример 1.9. ≈сли множество ј есть отрезок [1; 3], то множество  представл€ет собой объединение двух интервалов:
представл€ет собой объединение двух интервалов: 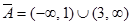 .
.
ќпределение 1.7. –азностью множеств ј и ¬ называетс€ множество —, состо€щее из всех элементов, принадлежащих множеству ј, но не принадлежащих ¬:
|
|
|
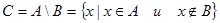 . .
| (1.5) |
ќпераци€ вычитани€ множеств не коммутативна:  .
»з определени€ разности множеств следует, что имеет место равенство .
»з определени€ разности множеств следует, что имеет место равенство  . .
| 
|
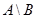
|
ѕример 1.10. ≈сли множество ј есть отрезок  , а множество ¬ есть отрезок
, а множество ¬ есть отрезок  , то разность
, то разность  представл€ет собой полуинтервал
представл€ет собой полуинтервал  , а
, а  полуинтервал
полуинтервал  .
.
ќпределение 1.8. —имметрической разностью множеств ј и ¬ называетс€ множество —, состо€щее из всех элементов, принадлежащих множествам ј и B, но не принадлежащих ихобщим област€м.
 . .
| (1.6) |
ƒругими словами симметрическа€ разность двух множеств  и и  состоит из элементов, которые принадлежат ровно одному из множеств: либо только состоит из элементов, которые принадлежат ровно одному из множеств: либо только  , либо только , либо только  . .
| 
|

| |
ќпераци€ симметрической разности дл€ трех множеств ассоциативна: 
| 
|

|
ѕример 1.11. ≈сли  ,
,  , то
, то  .
.
ќпределение 1.9. ƒекартовым произведением двух множеств ј и ¬ называетс€ множество —, состо€щее из всевозможных пар элементов  , у которых
, у которых 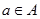 и
и  .
.

| (1.7) |
ѕример 1.12. ƒаны два множества:  ,
,  . ƒл€ этих множеств можно составить два варианта декартового произведени€ этих множеств:
. ƒл€ этих множеств можно составить два варианта декартового произведени€ этих множеств: 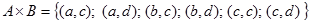 и
и 
»з примера видно, что множества  и
и  различны.
различны.
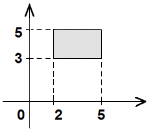
ѕример 1.13. ѕусть множество ј есть отрезок  ,на некоторой пр€мой, а множество ¬ есть отрезок ,на некоторой пр€мой, а множество ¬ есть отрезок  другой пр€мой. “огда декартово произведение другой пр€мой. “огда декартово произведение  , включающее многочисленные пары координат, составит пр€моугольник на плоскости. , включающее многочисленные пары координат, составит пр€моугольник на плоскости.
| 
|

|
ƒл€ двух конечных множеств  и
и  , мощности которых определены как
, мощности которых определены как  и
и  можно вычислить мощность декартового произведени€
можно вычислить мощность декартового произведени€  как
как
 . .
| (1.8) |






 ;
; Ø
Ø

