Два простых числа, которые отличаются на 2, как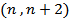 
получили образное название близнецы. В пределах первой сотни чисел расположены следующие пары близнецов: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73).
Все пары простых-близнецов, кроме (3, 5), имеют вид (
). По модулю 30[1] все пары близнецов, кроме первых двух, имеют вид (11, 13), или (17, 19), или (29, 31).
В натуральном ряду чисел можно выделить тройку близнецов типа 
например (3,5,7) или четверку близнецов вида 
, например (5, 7, 11, 13) или (11, 13, 17, 19).
Тройки различных простых чисел, разность между наибольшим и наименьшим из которых равна шести, называются числами-триплетами: (
) или (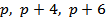
). Примеры триплетов: (5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (17, 19, 23).
Четверки простых чисел вида (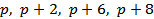
) называют квадруплетами: (5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109), (191, 193, 197, 199). По модулю 30 все квадруплеты, кроме первого, имеют вид (11, 13, 17, 19), а по модулю 210 имеют вид либо (101, 103, 107, 109), либо (191, 193, 197, 199).
Шестерки простых чисел вида (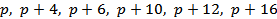
) называют секступлетами: (7, 11, 13, 17, 19, 23), (97, 101, 103, 107, 109, 113). По модулю 210 все секступлеты, кроме первого, имеют вид (97, 101, 103, 107, 109, 113).
Работа с простыми числами важна не только для чистой математики. В криптографии большие простые числа используются в алгоритмах шифрования с открытым ключом.
