18. 
19. 
20. 
21. 
22. 
23. 
24. 
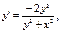
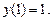
25. 
26. 
27. 
28. 
29. 
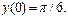
30. 
Задача 18. Розв’яжіть задачу Коші.
1. у' + ху = (1 + х) е– х у2, у(0) = 1.
2. ху' + у = 2у2 ln х, у(1) = 1/2.
3. 2 (ху' + у) = ху2, у(1) = 2.
4. у' + 4х3у = 4 (х3+1) е– 4х у2, у(0) = 1.
5. ху' – у = – у2 (ln х + 2) ln х, у(1) = 1.
6. 2 (у' + ху) = (1 + х) е– х у2, у(0) = 2.
7. 3 (ху' + у) = у2 ln х, у(1) = 3.
8. 2у' + у cos х = у –1 cos х (1+sin х), у(0) = 1.
9. у' + 4х3у = 4у2е4х (1 – х3), у(0) = – 1.
10. 3у' + 2ху = 2ху –2е–2х², у(0)=–1.
11. 2ху' – 3у = –(5х2 + 3) у3, у(1) = 1/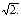 
12. 3ху' + 5у = (4х – 5) у4, у(1) = 1.
13. 2у' + 3y cos x = e2х (2 + 3 cos x) у –1, у(0) = 1.
14. 3 (ху' + у) = ху2, у(1) = 3.
15. у'–у = 2ху2, у(0) = 1/2.
16. 2ху' – 3у = –(20х2 + 12) у3, у(1) = 1/2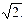 
17. у' + 2ху = 2х3у3, у(0) =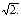
18. ху' + у = у2 ln х, у(1) = 1.
19. 2у' + 3у cos x = (8 + 12 cos х) е2ху –1, у(0) = 2.
20. 4у' + х3у = (х3 + 8) е–2х у2 , у(0) = 1.
21. 8ху' – 12у = – (5х2 + 3) у3, у(1) = 
22. 2 (у' + у) = ху2, у(0) = 2.
23. у' + ху = (х–1)еху2, у(0)=1.
24. 2у' – 3у cos х = –е–2х (2+3 cos x) у –1, у(0) = 1.
25. у' – у = ху2, у(0) =1.
26. 2 (ху' + у) = у2 ln х, у(1) = 2.
27. у' + у = ху2, у(0) = 1.
28. у' + 2у cth х = у2 ch х, у(1) = 1/sh 1.
29. 2 (у' + ху) = (х – 1) еху2, у(0) = 2.
30. у' – у tg x = –(2/3) y4 sin x, у(0) = 1.
31. ху' + у = ху2, у(1) = 1.
Задача 19. Розв’яжіть рівняння у повних диференціалах.
1. у′= 
2. у′= 
3. у′=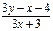 
4. у′= 
5. у′= 
6. у′= 
7. у'= 
8. у'= 
9. у'= 
10. у'= 
11. у'=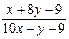 
12. у'= 
13. у'=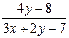 
14. у'= 
15. у'= 
16. у'= 
17. у'= 
18. у'= 
19. у'= 
20. у'= 
21. у'= 
22. у'= 
23. у'= 
24. у'= 
25. у'= 
26. у'= 
27. у'=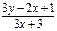 
28. у'= 
29. у'=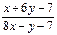 
30. у'= 
31. у'= 
Задача 20. Розв’яжіть рівняння у повних диференціалах.
1. 
2. 
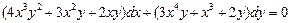
3. 
4. 
5. 
6. 
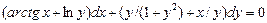
7. 
8. 
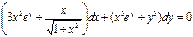
9. 
10. 
11. 
12. 
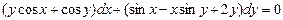
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
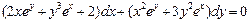
25. 
26. 
27. 
28. 
29. 
30. 
Задача 21. Знайти загальний інтеграл диференціального рівняння.
1. (3х2 + 4у2) dх + (8ху + еу) dу = 0.
2. (2х – 1 - 
) dх – (2у -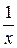 
) dу = 0.
3. (у2 + у sec2 х) dх + (2ху + tg х) dу = 0.
4. (3х2у + 2у +3) dх + (х3 + 2х + 3у2) dу = 0.
5. 
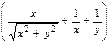dх +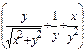 
dу = 0.
6. [ sin 2x – 2 cos (х + у)] dх – 2 cos (х +у) dу = 0.
7. (ху2 + х/у2) dх + (х2у – х2/у3) dу = 0.
8. 
dх - 
dу = 0.
9. 
dх - 
dу = 0.
10. 
dх + 
dу = 0.
11. 
dх + 
dу = 0.
12. 
= 0.
13. 
dх - 
dу = 0.
14. 
dх - 
dу = 0.
15. 
dх -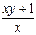 
dу = 0.
16. 
dх - 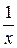dу = 0.
17. 
dх + (5х2+ 
)dу = 0.
18. 
dх - 
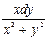=0.
19. еуdх + (cos у + хеу) dу = 0.
20. (у3+cos х) dх + (3ху2 + еу) dу = 0.
21. 
dх + (х2у 
+tg2 у) dу = 0.
22. (5ху2 – x3) dх + (5х2у – у) dу = 0.
23. [cos (х + у2) + sin х] dх + 2у cos (х + у2) dу = 0.
24. (х2 – 4ху – 2у2) dх + (у2 – 4ху – 2х2) dу = 0.
25. (sin у + у sin х + 
dх + (х cos y – cos x + 
dy = 0.
26. 
dх + 
dу = 0.
27. 
28. 2 (3ху2 + 2х3) dх + 3 (2х2у + у2) dу = 0.
29. (3х3 + 6х2у + 3ху2) dх + (2х3 + 3х2у) dу = 0.
30. ху2 dх + у (х2 + у2) dу = 0.
31. х dх + у dу + (х dу – у dх) / (х2 + у2) = 0.
Задача 22. Для даного диференціального рівняния методом ізоклін побудувати інтегральну криву, яка проходить через точку М.
1. у' = у – х2, М (1, 2). 2. уу' = –2х, М (0, 5).
3. у' = 2 + у2, М (1, 2). 4. у' = 
М (1, 1).
5. у' = (у – 1) х, М (1, 3/2). 6. уу' + х = 0, М (–2, –3).
7. у' = 3 + у2, М (1, 2). 8. ху' = 2у, М (2, 3).
9. у' (х2 + 2) = у, М (2, 2). 10. х2 – у2 +2хуу' = 0, М (2, 1).
11. у' = у – х, М (9/2, 1). 12. у' = х2 – у, М (1, 1/2).
13. у' = ху, М (0, –1). 14. у' = ху, М (0, 1).
15. уу' = – 
М (4, 2). 16. 2 (у + у') = х + 3, М (1, 1/2).
17. у' = х + 2у, М (3, 0). 18. ху' = 2у, М (1, 3).
19. 3уу' = х, М (–3, –2). 20. у' = у – х2, М (–3, 4).
21. х2 – у2 + 2хуу' = 0, М (–2, 1). 22.у' = х2 – у, М (2, 3/2).
23. у' = у – х, М (2, 1). 24. уу' = –х, М (2, 3).
25. у' = у – х, М (4, 2). 26. 3уу' = х, М (1, 1).
27. у' = х2 – у, М (0, 1). 28. у' = 3у 2/3, М(1, 3).
29. х2 – у2 + 2хуу' = 0, М (–2, –1). 30. у' = х (у – 1), М (1, 1/2).
31. у' = х + 2у, М(1, 2).
Задача 23. Складіть диференціальне рівняння та розв'яжіть його.
1. Тіло рухається прямолінійно зі швидкістю v = t2. Визначте закон руху тіла, якщо за перші 3 с тіло пройшло шлях 10 м.
2. Знайдіть функцію, графік якої проходить через точку А(4;3), якщо кутовий коефіцієнт дотичної до графіка цієї функції в будь-якій точці області її визначення обчислюється за формулою k = x -1/2.
3. Матеріальна точка масою т рухається під дією сили F вздовж осі ОХ протягом часу t. Запишіть диференціальне рівняння руху матеріальної точки, якщо сила, яка діє на точку, - величина стала.
4. Вздовж осі ОХ під дією сили F рухається матеріальна точка масою т протягом часу t. Запишіть диференціальне рівняння руху точки, якщо відомо, що сила періодично змінюється за законом F= F0sinωt.
5. Матеріальна точка здійснює гармонічне коливання з частотою ω= 2. Знайдіть її координату і швидкість у момент часу t=π/8, якщо при t0 = 0 координата і швидкість відповідно дорівнювали x(0) = 2, v(0) = 0.
6. Швидкість літального апарата змінюється за законом v(t)=2/5102t м/с. Визначте закон руху апарата, якщо за перші 2 с він пролетів шлях 4 м.
7. Точка рухається по прямій з прискоренням а. У початковий момент t = 0 точка має координату х і швидкість v. Знайдіть координату x(t) точки як функцію від часу.
8. 3 гвинтівки вистрілили вгору. Знайдіть закон руху кулі, вважаючи, що прискорення земного тяжіння 10 м/с2, швидкість вильоту кулі з гвинтівки 800 м/с (опором повітря знехтувати).
9. Швидкість розмноження бактерій пропорційна їхній кількості. У початковий момент при t= 0 було 100 бактерій, а за 3 год їхня кількість подвоїлася. Знайдіть залежність кількості бактерій від часу. У скільки разів збільшиться кількість бактерій за 9 год?
10. 3а рік кількість бактерій подвоюється, а швидкість розмноження прямо пропорційна наявній кількості бактерій. Складіть диференціальне рівняння розмноження бактерій.
11. Точка М рухається рівномірно по колу радіуса R, центр якого лежить у початку координат, з кутовою швидкістю ω. При t= 0 положення точки М характеризується кутом φ. Через деякий проміжок часу t положення точки М на колі характеризується кутом (ωt + φ). Знайдіть закон руху точки M.
12. Дослідом встановлено, що швидкість розпаду радію в кожний момент часу пропорційна початковій кількості. У початковий момент часу (t = 0) було R0 (г) радію. Складіть формулу для обчислення кількості радію в будь-який момент часу t.
13. Швидкість охолодження тіла в повітрі пропорційна різниці між температурою тіла і температурою повітря. Температура повітря 20°С. Протягом 20 хв тіло охолоджується від 100°С до 60°С. Визначте закон зниження температури тіла T від часу t.
14. Швидкість збільшення площі макового листка вікторії-регії, який має форму круга, пропорційна довжині кола листка і кількості сонячного світла, яке потрапляє на нього. Кількість світла пропорційна площі листка і косинусу кута між напрямом променів і вертикаллю до листка. Знайдіть залежність між площею S листка і часом t, якщо о 6-й годині ранку ця площа дорівнювала 1600 см2, о 18-й годині - 2500 см2, кут між напрямом променя сонця і вертикаллю о 6-й годині і о 18-й годині дорівнював 90°, а о 12-й годині - 0°.
15. За 15 років населення країни збільшилося в 1,2 рази. Через скільки років населення країни збільшиться в 1,5 раза?
16. Внаслідок розпаду 160 мг радіоактивної речовини через 50 хв залишилося 100 мг. Знайдіть період піврозпаду.
17. Коливання струни піаніно описується диференціальним рівнянням 
Знайдіть розв'язок цього рівняння, якщо f(0)=4, 
18. Знайдіть закон руху тіла по осі ОХ, якщо воно почало рухатися з точки А(4,0) зі швидкістю v = 2t +3t2.
19. Знайдіть закон руху тіла по осі OY, якщо воно почало рухатися з точки M(0;6) зі швидкістю v = 4t-6t2.
20. Складіть рівняння прямої, яка проходить через точку А(2:-3) і має дотичну з кутовим коефіцієнтом 4х - 3.
21. Радій В розпадається наполовину, утворюючи радіоактивний елемент радій С, протягом 26,7 хв. Знайдіть час розпаду 0,2 початкової кількості радію В.
22. Тіло з температурою 100°С помістили в повітряне середовище, температура якого 0°С, Через 20 хв температура тіла знизилась до 70°С. Через який час від початку охолодження температура дорівнюватиме 10°С?
23. У лабораторії було 5 г радіоактивної речовини з періодом піврозпаду 3 роки і 3 г іншої радіоактивної речовини. Який період піврозпаду цієї речовини, якщо через 12 років їх буде однаково?
24. Складіть рівняння кривої, відрізок довільної дотичної до якої між точкою дотику і віссю абсцис ділиться віссю ординат пополам.
25. Літак летить над Землею на висоті k зі швидкістю v км/год. На якій відстані х від точки А на Землі треба скинути з літака вантаж т (без початкової швидкості і нехтуючи опором повітря), щоб він потрапив у точку А?
26. Швидкість розпаду радію в кожен момент часу пропорційна його наявній масі. Знайдіть закон розпаду радію, якщо відомо, що в початковий момент t= 0 було т0 (г) радію і період піврозпаду цього елемента дорівнює 1590 років
27. Знайдіть найменшу швидкість, з якою має рухатися тіло вертикально вгору, щоб воно не повернулося на Землю (опором повітря знехтувати).
28. Знайдіть залежність між кількістю населення А і часом t, якщо в початковий момент було А населення, а через рік воно зросло на а (%),
29. Внаслідок реакції речовина А переходить у речовину В. Через 1 год після початку реакції залишилося 44,8 г речовини А, а через 3 год - 11,2 г цієї речовини. Визначте початкову кількість а речовини А та через який час залишиться половина цієї речовини.
30. Сповільнююча дія тертя води об гвинт катера пропорційна кутовій швидкості. В який момент часу швидкість обертання гвинта на холостому ходу дорівнюватиме 2 рад/с, якщо в момент пуску двигуна t = 0 він обертається з швидкістю 20 рад/с, а через 8 с - з швидкістю 16 рад/с?
31. Нехай температура повітря змінюється з висотою за законом dT/dh = -αT0, де Т0 - температура повітря на поверхні землі, α - сталий коефіцієнт. Знайдіть залежність тиску повітря від висоти.
Задача 24. Складіть диференціальне рівняння та розв'яжіть його.
1. Знайдіть рівняння кривої, яка проходить через точку М 0(2; 2) і має ту властивість, що ордината точки перетину нормалі з віссю ординат дорівнює добутку координат точки дотику.
2. Знайдіть криву, яка проходить через М 0(2; 1), якщо кутовий коефіцієнт дотичної в довільній точці кривої дорівнює квадрату ординати точки дотику.
3. Матеріальна точка масою m рухається прямолінійно під дією сили F, прямо пропорційної часу від початку руху і обернено пропорційної швидкості руху v. Встановіть залежність між швидкістю v і часом t, якщо 
при t = 0.
4. Швидкість точки, яка рухається прямолінійно, пропорційна кубу часу (коефіцієнт пропорційності дорівнює k). Через 2 с після початку руху точка буде на відстані 12 м. Знайдіть закон руху точки (тобто залежність шляху від часу).
5. Знайдіть рівняння лінії, яка перетинає вісь ординат у точці М0(0; 1), і кутовий коефіцієнт її дотичної в довільній точці дорівнює добутку абсциси на ординату точки дотику.
6. Знайдіть криву, яка проходить через точку М0 (2;1), якщо сума катетів трикутника, утвореного дотичною, ординатою точки дотику та віссю абсцис, дорівнює 3.
7. У посудину, яка містить 10л води, неперервно наливається зі швидкістю 2 л/хв розчин, у кожному літрі якого міститься 0,3 кг солі. Розчин, що наливається в посудину, перемішується з водою; утворена суміш витікає з посудини з тією самою швидкістю. Скільки солі буде в посудин через 5 хв?
8. Знайдіть криву, яка проходить через точку М0 ( 0; 2), якщо відрізок осі абсцис, який відтинається дотичною та нормаллю, проведеними з довільної точки кривої, дорівнює 4?
9. Посудина об'ємом 20 л містить повітря (80 % азоту та 20 % кисню). У посудину за кожну секунду надходить 0,1 л азоту, який неперервно змішується, і витікає така сама кількість суміші. Через який час у посудині буде 99 % азоту?
10. У посудину, яка містить 20 кг солі на 100 л суміші, кожну хвилину надходить 20 л води та витікає 10 л суміші. Визначте, яка кількість солі залишається в посудині через t хвилин.
11. Температура вийнятого з печі хліба протягом 20 хв падає від 100° до 60° С. Температура повітря 20° С. Визначте, через скільки часу від початку охолодження температура хліба стане 30° С, якщо швидкість охолодження тіла пропорційна різниці температур тіла та середовища.
12. Знайдіть криву, що проходить через точку М0 (1; 1/3), якщо кутовий коефіцієнт дотичної в довільній точці кривої втричі більший за кутовий коефіцієнт радіуса-вектора точки дотику.
13. Тіло рухається прямолінійно зі швидкістю v, що пропорційна квадрату часу. Знайдіть залежність між пройденим шляхом S і часом t, якщо S(0) = S0.
14. Знайдіть криві, в яких точка перетину довільної дотичної з віссю абсцис рівновіддалена від точки дотику і початку координат.
15. Точка масою т рухається прямолінійно. На точку діють сила, пропорційна часу, та сила протидії, пропорційна добутку швидкості на час. Знайдіть залежність швидкості від часу.
16. Знайдіть лінію, що проходить через точку М0 (3, 1), якщо ордината точки перетину дотичної з віссю ординат дорівнює подвоєній сумі координат точки дотику.
17. Знайдіть лінію, що проходить через точку М0 (1; 0), якщо ордината точки перетину дотичної з віссю ординат дорівнює добутку координат точки дотику.
18. Знайдіть лінії, в яких відстані від будь-якої дотичної до початку координат дорівнюють абсцисі точки дотику.
19. Знайдіть закон руху точки, що падає під дією сили ваги, якщо в початковий момент часу t=t 0 її висота h=h 0, а початкова швидкість v = v0.
20. Знайдіть рівняння кривої, яка проходить через точку М0 (4;3), якщо довжина відрізка нормалі від точки кривої до точки перетину з віссю ординат дорівнює 5.
21. Знайдіть лінії, для яких площа трикутника, утвореного дотичною, ординатою точки дотику та віссю абсцис, є величина стала, що дорівнює 25.
22. Відношення відрізка, який відтинає дотична до кривої на осі ординат, до відрізка, який відтинає ця сама дотична на осі абсцис, дорівнює подвоєній абсцисі точки дотику. Знайдіть рівняння таких кривих.
23. Точка рухається прямолінійно зі сталим прискоренням а. Знайдіть закон руху точки, якщо в початковий момент часу швидкість дорівнювала v0, а шлях — So.
24. Знайдіть лінію, що проходить через точку М0 (1; 0), яка має таку властивість: кут нахилу дотичної до осі Ох на 45° більший за кут між радіус-вектором точки дотику і віссю Ох.
25. Одиниця маси рухається вздовж осі абсцис під дією сталої сили F, яка спрямована вздовж осі. Сила опору повітря чисельно дорівнює швидкості руху. Знайдіть закон руху, якщо х(0)= x0, v(0)=v0.
26. Знайдіть криві, якщо квадрат довжини відрізка, що відтинає довільна дотична до цієї кривої від осі ординат, дорівнює добутку координат точки дотику.
27. Знайдіть криву, що проходить через точку М0 (0; 2), дотична до якої від осі абсцис відтинає відрізок, у два рази більший за ординату точки дотику.
