1. Робота з випереджальним завданням
Розгляньте рівняння:
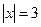 ;
;  ;
; 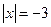 .
.
За відомим алгоритмом виконайте порівняння (додаток 2).
Висновки: 1) Усі наведені рівняння можна записати у вигляді одного рівняння  , де
, де 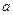 — будь-яке число.
— будь-яке число.
2) Спосіб розв’язування і кількість коренів цього рівняння залежить від знака числа 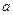 , а саме:
, а саме:

2. Розширення знань
Як було вже сказано на попередньому уроці, розв’язання багатьох рівнянь, що мають одну змінну, зводиться до розв’язування лінійних рівнянь з однією змінною. Серед таких рівнянь можна виділити:
а) рівняння з модулем;
б) рівняння, що містять дроби.
Далі розбираємо розв’язування рівнянь названих видів.
а) 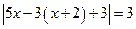 .
Перш ніж починати пояснення, слід активізувати мислення учнів, запропонувавши порівняти рівняння з рівнянням виду .
Перш ніж починати пояснення, слід активізувати мислення учнів, запропонувавши порівняти рівняння з рівнянням виду  .
• Чим відрізняється дане рівняння від рівняння .
• Чим відрізняється дане рівняння від рівняння  ?
• Чим схожі ці рівняння?
• Чим схожий спосіб розв’язування (перший крок) і чим буде відрізнятися розв’язування?
Після цього робимо записи в зошитах (проводимо усні зауваження) ?
• Чим схожі ці рівняння?
• Чим схожий спосіб розв’язування (перший крок) і чим буде відрізнятися розв’язування?
Після цього робимо записи в зошитах (проводимо усні зауваження)
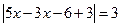 . (Спрощуємо вираз під знаком модуля.) . (Спрощуємо вираз під знаком модуля.)
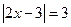 .
1) .
1)  або 2) або 2) 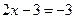 . (Оскільки . (Оскільки 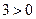 , ,  , , 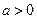 , то , то  або або 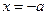 . Розв’язуємо лінійні рівняння.) . Розв’язуємо лінійні рівняння.)
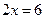 , , 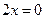 . .
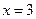 , , 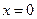 .
Відповідь. 3; 0. .
Відповідь. 3; 0.
| б) 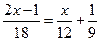 .
Перш ніж розв’язувати рівняння, слід порівняти його з іншими рівняннями, що були розв’язані раніше. Провести бесіду, розглянувши такі питання:
• Чим відрізняється дане рівняння від рівняння № 1 в домашньому завданні?
• Що спільного?
• Яку властивість рівносильних рівнянь можна використати, щоб позбутися дробів?
• Яка властивість дробів використовується при цьому?
Після цього можна записати розв’язання, додавши усні коментарі. .
Перш ніж розв’язувати рівняння, слід порівняти його з іншими рівняннями, що були розв’язані раніше. Провести бесіду, розглянувши такі питання:
• Чим відрізняється дане рівняння від рівняння № 1 в домашньому завданні?
• Що спільного?
• Яку властивість рівносильних рівнянь можна використати, щоб позбутися дробів?
• Яка властивість дробів використовується при цьому?
Після цього можна записати розв’язання, додавши усні коментарі.
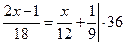 . (Знайдемо НСК (18; 12; 9) = 36 та помножимо на нього обидві частини рівняння.) . (Знайдемо НСК (18; 12; 9) = 36 та помножимо на нього обидві частини рівняння.)
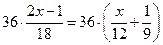 . (Виконаємо множення.) . (Виконаємо множення.)
 . .
 ; ;  . (Виконаємо рівносильні перетворення, зведемо рівняння до лінійного і розв’яжемо його.) . (Виконаємо рівносильні перетворення, зведемо рівняння до лінійного і розв’яжемо його.)
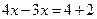 , ,  .
Відповідь. 6. .
Відповідь. 6.
|
Висновки. Розібравши приклади а) та б) ми впевнилися в тому, що деякі рівняння з модулем, так само як і деякі рівняння з дробами (не всі!!!), шляхом виконання рівносильних перетворень та використання властивостей чисел можуть бути зведені до лінійних рівнянь з однією змінною.






