1) Обчисліть: 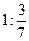 ;
; 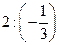 ;
; 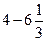 ;
; 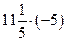 .
.
2) Спростіть вираз:
а) 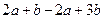 ; б)
; б) 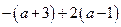 ; в)
; в) 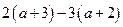 ; г)
; г) 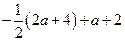 .
.
IV. Повторення, поглиблення та систематизація знань
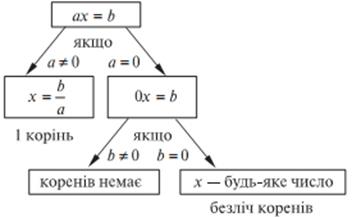
Поняття лінійного рівняння з однією змінною є принципово новим для учнів (новим є і сам підхід до класифікації не за дією, що зв’язує компоненти рівняння, а за способом розв’язування).
Хоча фактично всі рівняння, що їх розв’язували учні в молодших класах, є рівняння, що зводяться до лінійних, однак відповідна термінологія вводиться вперше. Під час дослідження питання про кількість розв’язків лінійного рівняння  при різних
при різних  і
і  виділяємо три випадки:
виділяємо три випадки:
1) 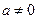 і
і  будь-яке;
будь-яке;
2)  ;
; 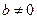 ;
;
3)  ;
;  .
.
Із першим випадком учні вже зустрічались, другий і третій є для них новими. Переходячи від теоретичного матеріалу до розв’язування рівнянь із застосовуванням названих вище міркувань, треба пояснити (показати на прикладах), в якому випадку ми дістаємо рівняння виду 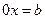
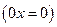 , бо дуже часто учні не розуміють, як і чому під час розв’язування рівняння, наприклад,
, бо дуже часто учні не розуміють, як і чому під час розв’язування рівняння, наприклад, 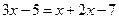 ми дістаємо рівняння
ми дістаємо рівняння 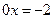 і найголовніше: мотивація (з неї і слід почати цей етап уроку). На багатьох прикладах різних видів рівнянь треба показати, що лінійні рівняння є основою цих рівнянь.
і найголовніше: мотивація (з неї і слід почати цей етап уроку). На багатьох прикладах різних видів рівнянь треба показати, що лінійні рівняння є основою цих рівнянь.
План викладення матеріалу
1. Робота з випереджальним домашнім завданням (мотивація).
2. Означення лінійного рівняння з однією змінною.
3. Схема розв’язування лінійних рівнянь з однією змінною.
4. Приклади рівнянь, що зводяться до лінійних і схема їх розв’язування.
Результатом обговорення можуть бути такі записи в зошитах учнів:
Конспект 2
Лінійні рівняння з однією змінною
1. Розв’язуючи рівняння, під час рівносильних перетворень ми дістаємо рівняння, що можна записати в одному вигляді, якщо записати числа буквами, а саме:  .
.
2. Рівняння виду  , де
, де  і
і  — числа, а
— числа, а  — невідоме, називається лінійним рівнянням з одним невідомим.
— невідоме, називається лінійним рівнянням з одним невідомим.
Наприклад: 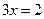 ;
; 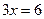 ;
; 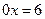 ;
; 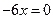 ;
; 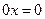 ;
; 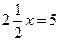 .
.
3. Схема розв’язування лінійного рівняння виду  .
.
4. а) 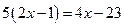 ; ;
| б) 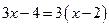 ; ;
| в) 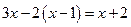
|
Шляхом рівносильних перетворень зводимо рівняння до виду  , а далі за схемою: , а далі за схемою:
| ||
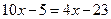 ; ;
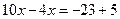 ; ;
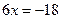 ; ;
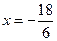 ; ;
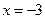 Відповідь. -3
Відповідь. -3
| 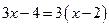 ; ;
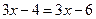 ; ;
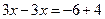 ; ;
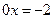 Відповідь. Коренів немає
Відповідь. Коренів немає
| 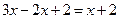
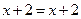
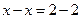
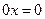 Відповідь.
Відповідь.  — будь-яке число — будь-яке число
|
Зауважимо: 1) Під час розв’язування рівняння  при
при 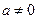 поширеною є така помилка учнів: спроба знаходження
поширеною є така помилка учнів: спроба знаходження  як частки у вигляді цілого числа або десяткового дробу (часто чуємо, що
як частки у вигляді цілого числа або десяткового дробу (часто чуємо, що 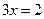 не розв’язується, бо
не розв’язується, бо 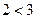 ). Тому, застосовуючи алгоритм, наголошуємо, що при
). Тому, застосовуючи алгоритм, наголошуємо, що при 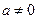 корінь
корінь 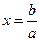 — існує завжди, не залежно від співвідношення
— існує завжди, не залежно від співвідношення  та
та  , і може бути як натуральним, так і цілим числом або дробом — звичайним чи десятковим. Але, щоб не виконувати зайвих дій, (окрім випадків, коли ділення найкраще виконується усно) корінь
, і може бути як натуральним, так і цілим числом або дробом — звичайним чи десятковим. Але, щоб не виконувати зайвих дій, (окрім випадків, коли ділення найкраще виконується усно) корінь  треба записувати спочатку саме як дріб, а потім вже використовувати набуті в 6 класі вміння перетворювати дроби.
треба записувати спочатку саме як дріб, а потім вже використовувати набуті в 6 класі вміння перетворювати дроби.
2) У прикладах 4 (б, в) дуже важливо, щоб учні зрозуміли, звідки береться  у лівій частині лінійного рівняння. Тому актуалізація знань (див. вище) є дуже важливим елементом уроку.
у лівій частині лінійного рівняння. Тому актуалізація знань (див. вище) є дуже важливим елементом уроку.
V. Закріплення знань, формування вмінь
Однією з програмних вимог до рівня загальноосвітньої підготовки учнів є вміння розпізнавати лінійні рівняння серед даних рівнянь, наводити приклади лінійних рівнянь та розв’язувати лінійні рівняння з однією змінною та ті, що до них зводяться.
Тому в системі завдань до уроку бажано виділити завдання таких типів:
1) на розпізнавання лінійних рівнянь та на складання лінійних рівнянь за певними умовами;
2) на розв’язування лінійного рівняння та простіших рівнянь, що зводяться до лінійних шляхом рівносильних перетворень.






