Восьмое уравнение Максвелла представляет собой обобщение опытных данных по изучению электрического тока. В интегральном виде это уравнение представляет собой закон Ома для полной цепи и записывается в виде:
(2.58)
Здесь 
- электродвижущая сила источника тока, 
- сопротивление внешней части цепи, 
- внутреннее сопротивление цепи или сопротивление источника тока.
Для того чтобы получить восьмое уравнение Максвелла в дифференциальном виде, рассмотрим подробнее понятие электрического тока. Электрическим током называется любое направленное движение электрических зарядов. Такой ток часто называют током проводимости.
Рассматривая роль среды при исследовании электромагнитных явлений, Фарадей ввел понятие вектора электрической индукции 
, который первоначально назывался вектором электростатического смещения.
Когда Максвелл придавал идеям Фарадея математическую форму, он ввел понятие тока смещения. Ток смещения вместе с током проводимости образуют полный ток в цепи.
Чтобы пояснить понятие тока смещения, рассмотрим конденсатор в электрической цепи. Если электрическая цепь является цепью постоянного тока, то конденсатор представляет собой разрыв в цепи. Однако, если электрическая цепь является цепью переменного тока, то через конденсатор проходит ток, который и является током смещения. Ток смещения связан с поляризацией диэлектрика, находящегося внутри конденсатора, или связан с переменным электрическим полем.
Для того, чтобы получить выражение для тока смещения, воспользуемся седьмым уравнением Максвелла и запишем силу тока в интегральной форме:
(2.59)
Силу тока выразим через плотность тока:
(2.60)
Заряд в правой части формулы (2.59) запишем, используя теорему Гаусса:
(2.61)
Подставляем формулы (2.60) и (2.61) в формулу (2.59):
(2.62)
В правой части выражения (2.62) поменяем местами операции дифференцирования и интегрирования, тогда получаем:
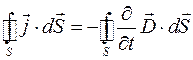(2.63)
Формула (2.63) преобразуется в выражение:
(2.64)
Из формулы (2.64) следует, что величина 
представляет собой плотность некоторого тока, который и назван током смещения:
(2.65)
Тогда формула (2.64), представляющая собой закон сохранения заряда, будет иметь вид:
(2.66)
Из формулы (2.66) следует, что суммарная плотность тока равна сумме плотности тока проводимости и тока смещения:
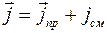(2.67)
Используя понятие плотности тока и классические представления об электропроводности, можно получить восьмое уравнение Максвелла в дифференциальной форме:
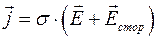(2.68)
Здесь 
- удельная проводимость, которая связана с удельным сопротивлением проводников 
формулой 
(2.69)
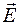- напряженность электрического поля, созданного электрическими зарядами, 
- напряженность поля, созданного сторонними силами, обусловленными химическими, термическими и другими процессами.
