ЭЛЕКТРОДИНАМИКА
УРАВНЕНИЯ МАКСВЕЛЛА
Учебно–методическое пособие для студентов
физико-математических и инженерных специальностей
ВЕЛИКИЙ НОВГОРОД
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИМЕНИ ЯРОСЛАВА МУДРОГО
Самолюк Н.П.
ЭЛЕКТРОДИНАМИКА
УРАВНЕНИЯ МАКСВЕЛЛА
Учебно–методическое пособие для студентов
физико-математических и инженерных специальностей
ВЕЛИКИЙ НОВГОРОД
УДК 53 (0765)
Рецензент: кандидат физико-математических наук, доцент Витов В.Ф.
Пособие содержит подробное изложение системы уравнений Максвелла в дифференциальном и интегральном виде. Материал пособия соответствует содержанию курса общей физики для студентов инженерных и физико-математических специальностей
Электродинамика. Уравнения Максвелла. Учебно–методическое пособие для студентов физико-математических и инженерных специальностей по теме: «Уравнения Максвелла». /Сост. Н.П. Самолюк. - НовГУ им. Ярослава Мудрого. – Новгород, 2011. – 26 с.
©Новгородский государственный
университет, 2011
© Н.П.Самолюк
составление, 2011
СОДЕРЖАНИЕ
1. Краткая история……………………………………………………………. 5
2. Каноническая форма ………………………………………………………. 6
2.1. Первое уравнение Максвелла……………………………………………. 6
2.2. Второе уравнение Максвелла……………………………………………. 8
2.3. Третье уравнение Максвелла…………………………………………….. 11
2.4. Четвертое уравнение Максвелла................................................................13
2.5 и 2.6. Пятое и шестое уравнения Максвелла……………………………..19
2.7. Седьмое уравнение Максвелла…..……………………………………….20
2.8. Восьмое уравнение Максвелла………..………………………………….23
3. Полная система уравнений Максвелла…………………………………….25
Уравнения Максвелла
Краткая история
Формулировке уравнений Максвелла предшествовали открытия законов взаимодействий заряженных тел, намагниченных тел и проводников с электрическим током. При этом были сформулированы закон Кулона, закон Ампера, закон Био Савара – Лапласа.
В 1831 M. Фарадей открыл явление электромагнитной индукции и сформулировал закон, описывающий это явление. Кроме того, примерно в то же время он ввёл понятие электрического и магнитного поля как самостоятельных физических субстанций.
Опираясь на представление Фарадея о поле, и введя ток смещения, равнозначный по своему магнитному действию обычному электрическому току, Дж. К. Максвелл сформулировал систему уравнений, названную впоследствии уравнениями Максвелла.
Уравнения Максвелла функционально связывают электрическое и магнитное поле с зарядами и токами и охватывают собой все известные закономерности электромагнетизма. Первоначально Максвелл прибегал к вспомогательным механическим моделям "эфира", но уже в "Трактате об электричестве и магнетизме" (1873) электромагнитное поле рассматривалось как самостоятельный физический объект.
Физической основой уравнений Максвелла является принцип близкодействия, утверждающий, что передача электромагнитных возмущений от точки к точке происходит с конечной скоростью (в вакууме со скоростью света с). Этот принцип противоположен классическому ньютоновскому принципу дальнодействия, сводящемуся к мгновенной передаче воздействий на любое расстояние 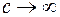 .
.
Математическим аппаратом теории Максвелла является векторный анализ. Максвелл считал, что его заслуга состоит лишь в математическом оформлении идей Фарадея.






