На цьому етапі для отримання значень відрізків 
, на яких розміщений єдиний корінь можуть застосовуватися:
а) аналітичні методи;
б) режим табулювання функції 
;
в) графічний метод.
6.2.1. Аналітичні методи порівняно просто застосовувати для алгебраїчних рівнянь. Нижню та верхню межу всіх коренів для таких рівнянь можна визначити з допомогою правила кільця:
Нехай 
тоді всі корені знаходяться в кільці 
, де 
.
Розглянемо правило для рівняння 
; 
; 
; 
.
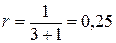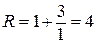Таким чином, всі додатні корені даного рівняння знаходяться в діапазоні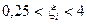 
, а від’ємні в інтервалі 
.
Для трансцендентних рівнянь аналітичний метод відокремлення коренів має таку послідовність:
а) знаходять область існування коренів;
б) обчислюють і визначають критичні точки 
;
в) записують інтервали, для яких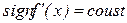 
;
г) досліджують знаки функції на кінцях інтервалів;
д) виписують відрізки ізоляції коренів.
Наприклад, маємо рівняння 
:
а) область існування функції: 
;
б) 
| х | 0,5 | 1,5 | |
| - | + |
в)
г) 
Отже, рівняння має два кореня в інтервалах 
та 
.
6.2.2. Аналітичний спосіб отримання меж відокремлення коренів дає досить широкі інтервали 
. А тому їх в подальшому уточнюють методом табуляції 
або графічним методом.
Табулювання функції заключається в послідовному аналізі зміни знака функції в деякому інтервалі зміни х (найчастіше з постійним кроком). В тих місцях, де функція змінює свій знак, повинен бути корінь. По критерію (6.2) уточнюють його відокремленість.
Застосуємо принцип табуляції для рівняння .
Раніше ми вияснили, що всі корені цього рівняння знаходяться в інтервалі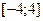 
. Табулюємо цей діапазон з кроком 
:
| х | -4 | -3 | -2 | -1 | |||||
| у | - | - | - | + | + | - | - | + | + |
Отже, маємо один від’ємний корінь в інтервалі 
та два додатніх в інтервалах 
та 
.
Для розглянутого раніше трансцендентного маємо:
| х | 0,01 | 0,5 | … | 2,5 | 3,5 | |||
| у | - | + | + | + | + | + | - | - |
Тут два кореня в діапазонах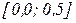 
та 
.
6.2.3. Графічний метод відокремлення коренів дає наочне представлення знаходження коренів рівняння. Найчастіше при реалізації цього методу функцію 
представляють у вигляді 
таким чином, щоб порівняно легко можна було на координатній площині зобразити графіки 
та 
. Тоді точка перетину цих графіків буде давати наближене значення кореня. Вибравши ліворуч та праворуч від такої точки перетину точки a та b, перевіряють знаходження всередині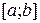 
кореня по критерію (6.1) і можна переходити до його уточнення. На рисунку 21 зображені точки перетину графіків 
та 
для першого розглянутого прикладу, та 
і 
для другого.
 |
Рисунок 21 – Графічний спосіб відокремлення коренів
