Тема 6. Розв’язок нелінійних рівнянь та їх систем
Нелінійним рівнянням 
називається рівняння, графічне представлення якого 
являє собою криву лінію.
В залежності від того, які функції входять в рівняння , їх поділяють на алгебраїчні та трансцендентні. Рівняння вважається алгебраїчним, якщо для одержання значення функції 
по заданому значенню х, потрібно виконувати лише арифметичні дії та піднесення до степені з раціональним показником. Алгебраїчне рівняння завжди можна привести до вигляду: 
.
Наприклад: 
, що після перетворення має вигляд 
.
Якщо в склад функції входять функції показникові (
), логарифмічні (
, тригонометричні (
) та інші, то таке рівняння називається трансцендентним.
Приклад: 
.
Коренем нелінійного рівняння є таке значення 
, яке при підстановці його в 
перетворює рівняння в нуль. В залежності від вигляду корені можуть бути як дійсними числами, так і комплексно-спряженими. При обчисленні нелінійних рівнянь нас будуть цікавити дійсні корені. Графічно дійсні корені являють собою точки на осі ОХ координатної площини, в яких графік функції перетинає цю вісь (рисунок 19).
Рисунок 19 – Корені рівняння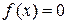 
Порівняно з трансцендентними рівняннями, для алгебраїчних рівнянь завжди відомо точну кількість їх коренів. Наведемо деякі властивості алгебраїчних рівнянь, що допомагають в їх дослідженні:
а) алгебраїчне рівняння n -ого порядку має n коренів, які можуть бути, як дійсними так і комплексними;
б) кількість додатніх коренів дорівнює кількості змін знаків у послідовності коефіцієнтів 
(або менше на ціле число – нульові коефіцієнти не враховуються);
в) кількість від’ємних коренів дорівнює (або менша на ціле число) числу змін знаків коефіцієнтів при зміні х на – х.
Із курсу математичного аналізу згадаємо дві теореми:
1. Якщо функція на відрізку 
неперервна і набуває на кінцях цього відрізка різних знаків, то в середині цього відрізка існує принаймні один корінь рівняння :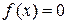
(6.1)
2. Якщо функція має похідну, що не змінює знака на відрізку , то при виконанні умови попередньої теореми рівняння 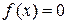має на цьому відрізку єдиний (відокремлений) корінь:
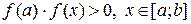(6.2).
Зміст цих теорем демонструє рисунок 20.
Рисунок 20 – Умови існування відокремленого кореня
Будемо використовувати критерії (6.1) та (6.2) при знаходженні коренів рівняння 
.
Процес їх одержання поділяється на два етапи:
1. На етапі відокремлення коренів на осі ОХ знаходяться такі відрізки 
в середині яких знаходиться єдиний корінь.
2. На етапі уточнення коренів діапазон звужують допоки значення функції в звуженому діапазоні з заданою точністю не стане рівним нулю.
