Функция f(x) в точке x 1 имеет максимум (maximum), если f(x 1 + ∆x) < f(x 1 ) при любых ∆x (положительных и отрицательных), достаточно малых по абсолютной величине, т.е. если значение функции f(x) в точке x 1 больше, чем ее значение во всех точках некоторого интервала, содержащего точку x 1.
Определение 3
Функция f(x) имеет минимум (minimum) при x=x 2, если f(x 2 +∆x) > f(x 2 ) при любых ∆x – как положительных, так и отрицательных, достаточно малых по абсолютной величине.
В связи с определениями максимума и минимума следует обратить внимание на следующие обстоятельства.
1. Функция, определенная на отрезке, может достигать максимума и минимума только при значениях x, заключенных внутри рассматриваемого отрезка.
2. Не следует думать, что максимум и минимум функции являются соответственно ее наибольшими и наименьшими значениями на рассматриваемом отрезке: в точке максимума функция имеет наибольшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке максимума, а в точке минимума – наименьшее значение лишь по сравнению с теми значениями, которые она имеет во всех точках, достаточно близких к точке минимума.
Максимумы и минимумы функции называются экстремумами или экстремальными значениями функции.
Экстремальные значения функции и их расположение на отрезке [ а, b ] в известной степени характеризуют изменение функции в зависимости от изменения аргумента.
Ниже будет указан метод нахождения экстремальных значений.
Теорема 3 (необходимое условие существования экстремума)
Если дифференцируемая функция y= f(x) имеет в точке x=x 1 максимум или минимум, то ее производная обращается в нуль в этой точке, т.е. f'(x) =0.
Доказательство. Предположим для определенности, что в точках x=x1 функция имеет максимум. Тогда при достаточно малых по абсолютному значению приращениях ∆x (∆x≠0) имеет место f(x1+ ∆x) < f(x1), т.е. f(x1+ ∆x) - f(x1) < 0. Но в таком случае знак отношения
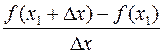
определяется знаком ∆ x, а именно:
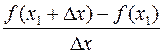> 0, при ∆ x <0,
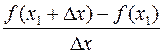<0, при ∆ x <0.
