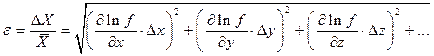Расчет погрешностей косвенных измерений

Как уже указывалось, косвенные измерения физической величины определяются прямыми измерениями других физических величин, которые находятся в определенной функциональной зависимости от искомой величины. Для определения надежности результата косвенных измерений необходимо применять распределение вероятностей рассматриваемой функции. Однако, такой строгий подход во многих случаях можно заменить упрощенным.

Пусть искомая величина Х является функцией только одной переменной, т.е. , причем, х определяется из прямых измерений 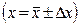. При изменении х на dх произойдет изменение функции Х на dX. Применяя разложение функции 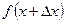в ряд Тейлора:

,

откуда

Заменяя значок дифференциала d значком ошибки D, получаем формулу для абсолютной погрешности результата косвенных измерений:

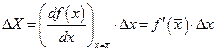
Окончательный результат можно представить в виде:

Относительная погрешность равна:

Пусть Х является функцией нескольких переменных, т.е. X = f (x, y, z). Для каждой величины x, y, z,…мы имеем в результате прямых измерений следующие данные: 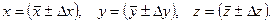Доверительные интервалы D x, D y, D z для прямых измерений находятся методом, указанном в порядке обработки результатов прямых измерений, придерживаясь строгого правила: все доверительные интервалы D x, D y, D z определяются в соответствии с табл. 2 для одного и того же значения доверительной вероятности a. Оценка доверительного интервала D C в этом случае, как это следует из теории [1, 2, 4], производится по формуле:

где 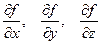- частные производные f (x, y, z, …) по переменным x, y, z соответственно, вычисленные для их средних значений.

Частная производная функции многих переменных по одной переменной, скажем х, является обычной производной функции по х, причем все остальные переменные y, z,… считаются постоянными параметрами. Относительную ошибку величины Х легко вычислить, написав

Так как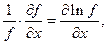

то для относительной погрешности получаем: