В случае большого числа измерений (
), случайный разброс значений измеряемой величины подчиняется закону,
 |
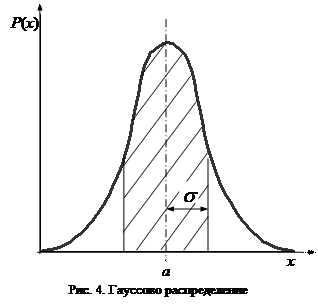открытому Гауссом. Функция P (X) симметрична относительно а, достигает максимума при Х = а (рис.4).
Кроме параметра а функция P (X) задается еще параметром s, который называется стандартным отклонением.
Величина D = s 2 называется дисперсией распределения и имеет смысл среднего значения квадрата отклонения Х от истинного значения а, т.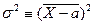е. 
, где 
— средний квадрат отклонения измеряемой величины от истинного значения.
Р (Х) быстро стремится к нулю, когда Х становится большим по сравнению с s.
Функция нормального распределения имеет вид:
(1)
Из рис. 5 видно, что основная часть результатов измерений группируется около центрального значения а – истинного значения измеряемой величины.
Отклонения по обе стороны от центра распределения наблюдаются тем реже, чем больше абсолютная величина таких отклонений.
Если изменить метод измерения величины а и измерять ее другим прибором, например, более совершенным, более точным, то разброс результатов измерений будет около центра с прежней абсциссой а, но разброс результатов существенно уменьшится (рис. 5, кривая 1). Если же точность метода измерений ниже, чем для кривой 2, то разброс результатов увеличится и кривая станет более пологой (рис. 5, кривая 3). Трем кривым на рис. 5 соответствуют разные значения стандарта отклонения s, который характеризует размах (разброс) случайных отклонений, присущих данному методу измерения. При этом площадь под кривыми распределения для разных s одна и та же. Параметры а и s в распределении Гаусса, как правило, неизвестны и их нужно искать по данным значениям Х 1, Х 2, … Хn, полученным из опыта. В теории погрешностей существует метод (максимального правдоподобия), который позволяет установить связь между параметрами распределения Гаусса а и s и набором результатов измерений физической величины. Используя этот метод, можно строго математически доказать, что наиболее правдоподобной оценкой истинного значения измеряемой величины является среднее арифметическое из данных измерений, т.е.
(2)
а наилучшей оценкой второго параметра s является средняя квадратичная погрешность среднего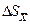 
.
Расчет осуществляется по формуле:
(3)
